
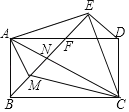
【题目】如图,以矩形ABCD对角线AC为底边作等腰直角△ACE,连接BE,分别交AD,AC于点F,N,CD=AF,AM平分∠BAN.下列结论:①EF⊥ED;②∠BCM=∠NCM;③AC=![]() EM;④BN2+EF2=EN2;⑤AEAM=NEFM,其中正确结论的个数是( )
EM;④BN2+EF2=EN2;⑤AEAM=NEFM,其中正确结论的个数是( )
A.2B.3C.4D.5
【答案】C
【解析】
①正确,只要证明A,B,C,D,E五点共圆即可解决问题;
②正确,证明BE平分∠ABC,再证明点M是△ABC的内心即可;
③正确,证明∠EAM=∠EMA可得EM=AE,即可解决问题;
④正确.如图2中,将△ABN逆时针旋转90°得到△AFG,连接EG.想办法证明△GEF是直角三角形,利用勾股定理即可解决问题;
⑤错误.利用反证法证明即可.
解:如图1中,连接BD交AC于O,连接OE.
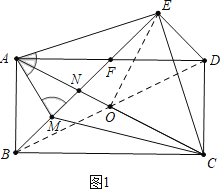
∵四边形ABCD是矩形,
∴OA=OC=OD=OB,
∵∠AEC=90°,
∴OE=OA=OC,
∴OA=OB=OC=OD=OE,
∴A,B,C,D,E五点共圆,BD是直径,
∴∠BED=90°,
∴EF⊥ED,故①正确,
∵CD=AB=AF,∠BAF=90°,
∴∠ABF=∠AFB=∠FBC=45°,
∴BM平分∠ABC,
∵AM平分∠BAC,
∴点M是△ABC的内心,
∴CM平分∠ACB,
∴∠MCB=∠MCA,故②正确,
∵∠EAM=∠EAC+∠MAC,∠EMA=∠BAM+∠ABM,∠ABM=∠EAC=45°,
∴∠EAM=∠EMA,
∴EA=EM,
∵△EAC是等腰直角三角形,
∴AC=![]() EA=
EA=![]() EM,故③正确,
EM,故③正确,
如图2中,将△ABN绕点A逆时针旋转90°,得到△AFG,连接EG,

∵将△ABN绕点A逆时针旋转90°,得到△AFG,
∴∠NAB=∠GAF,∠GAN=∠BAD=90°,AG=AN,GF=BN,
∵∠EAN=45°,
∴∠EAG=∠EAN=45°,
∵AE=AE,
∴△AEG≌△AEN(SAS),
∴EN=EG,
∵∠AFG=∠ABN=∠AFB=45°,
∴∠GFB=∠GFE=90°,
∴EG2=GF2+EF2,
∴BN2+EF2=EN2,故④正确,
不妨设AEAM=NEFM,
∵AE=EC,
∴![]() ,
,
∴只有△ECN∽△MAF才能成立,
∴∠AMF=∠CEN,
∴CE∥AM,
∵AE⊥CE,
∴MA⊥AE(矛盾),
∴假设不成立,故⑤错误,
故选:C.


科目:初中数学 来源: 题型:
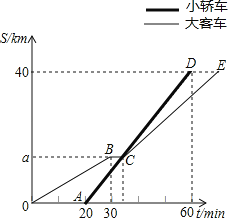
【题目】某班同学从学校出发去太阳岛春游,大部分同学乘坐大客车先出发,余下的同学乘坐小轿车20分钟后出发,沿同一路线行驶.大客车中途停车等候5分钟,小轿车赶上来之后,大客车以原速度的![]() 继续行驶,小轿车保持速度不变.两车距学校的路程S(单位:km)和大客车行驶的时间t(单位:min)之间的函数关系如图所示.下列说法中正确的个数是( )
继续行驶,小轿车保持速度不变.两车距学校的路程S(单位:km)和大客车行驶的时间t(单位:min)之间的函数关系如图所示.下列说法中正确的个数是( )
①学校到景点的路程为40km;
②小轿车的速度是1km/min;
③a=15;
④当小轿车驶到景点入口时,大客车还需要10分钟才能到达景点入口.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一条道路上,甲车从![]() 地到
地到![]() 地,乙车从
地,乙车从![]() 地到
地到![]() 地,两车同时出发以各自速度匀速行驶. 两车相遇后,乙车休息了
地,两车同时出发以各自速度匀速行驶. 两车相遇后,乙车休息了![]() 小时,然后继续原速驶往
小时,然后继续原速驶往![]() 地,图中的折线段表示甲、乙两车之间的距离
地,图中的折线段表示甲、乙两车之间的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)的函数关系的图象,下列说法错误的是( )
(小时)的函数关系的图象,下列说法错误的是( )
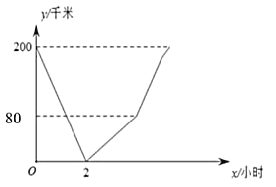
A.甲乙两车出发![]() 小时后相遇B.甲车速度是
小时后相遇B.甲车速度是![]() 千米/小时
千米/小时
C.甲车到![]() 地比乙车到
地比乙车到![]() 地早
地早![]() D.相遇时乙车距离
D.相遇时乙车距离![]() 地
地![]() 千米
千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年初,武汉爆发了新型冠状病毒引起的肺炎,并迅速在全国传染开来,与此同时医护人员一直坚守在抗击肺炎的前线,为我们保驾护航!罗曼罗兰说:“凡是行为善良与高尚的人,定能因之而担当患难.”他们是最可亲可敬的人!由此,医疗物资护目镜的需求量大大增加,两江新区某护目镜生 产厂家自正月初三起便要求全体员工提前返岗,在接到单位的返岗通知后,员工们都毫无怨言,快速回到了自己的工作岗位,用自己的实际行动践行着一份责任和担当.已知该厂拥有两条不同的护目镜加工生产线
年初,武汉爆发了新型冠状病毒引起的肺炎,并迅速在全国传染开来,与此同时医护人员一直坚守在抗击肺炎的前线,为我们保驾护航!罗曼罗兰说:“凡是行为善良与高尚的人,定能因之而担当患难.”他们是最可亲可敬的人!由此,医疗物资护目镜的需求量大大增加,两江新区某护目镜生 产厂家自正月初三起便要求全体员工提前返岗,在接到单位的返岗通知后,员工们都毫无怨言,快速回到了自己的工作岗位,用自己的实际行动践行着一份责任和担当.已知该厂拥有两条不同的护目镜加工生产线![]() .原计划
.原计划![]() 生产线每小时生产护目镜
生产线每小时生产护目镜![]() 个,
个,![]() 生产线每小时生产护目镜
生产线每小时生产护目镜![]() 个.
个.
(1)若生产线![]() 一共工作
一共工作![]() 小时,且生产护目镜的总数量不少于
小时,且生产护目镜的总数量不少于![]() 个,则
个,则![]() 生产线至少生产护目镜多少小时?
生产线至少生产护目镜多少小时?
(2)原计划![]() 生产线每天均工作
生产线每天均工作![]() 小时,但现在为了尽快满足我市护目镜的需求,两条生产线每天均比原计划多工作了相同的小时数,但因为机器损耗及人员不足原因,
小时,但现在为了尽快满足我市护目镜的需求,两条生产线每天均比原计划多工作了相同的小时数,但因为机器损耗及人员不足原因,![]() 生产线每增加
生产线每增加![]() 小时,该生产线每小时的产量将减少
小时,该生产线每小时的产量将减少![]() 个,
个,![]() 生产线每增加
生产线每增加![]() 小时,该生产线每小时的产量将减少
小时,该生产线每小时的产量将减少![]() 个.这样一天生产的护目镜将比原计划多
个.这样一天生产的护目镜将比原计划多![]() 个,求该厂实际每天生产护目镜的时间.
个,求该厂实际每天生产护目镜的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a≠0)与x轴交于原点及点A,且经过点B(4,8),对称轴为直线x=﹣2,顶点为D.
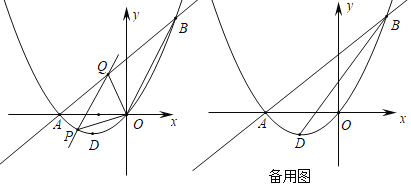
(1)填空:抛物线的解析式为 ,顶点D的坐标为 ,直线AB的解析式为 ;
(2)在直线AB左侧抛物线上存在点E,使得∠EBA=∠ABD,求E的坐标;
(3)连接OB,点P为x轴下方抛物线上一动点,过点P作OB的平行线交直线AB于点Q,当S△POQ:S△BOQ=1:2时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
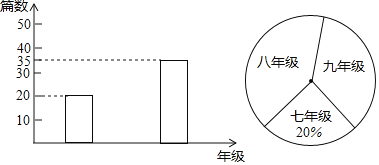
【题目】池州十中组织七、八、九年级学生参加“中国梦”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了以下两幅不完整的统计图,根据图中提供的信息完成以下问题:
(1)全校参赛作文篇数为 篇,补全条形统计图;
(2)扇形统计图中九年级参赛作文篇数对应的圆心角是 ;
(3)经过评审,全校共有4篇作文荣获一等奖,其中一篇来自七年级,两篇来自八年级,一篇来自九年级,学校准备从一等奖作文中任选两篇刊登在校刊上,请用树状图方法求出九年级一等奖作文登上校刊的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 平分
平分![]() .
.
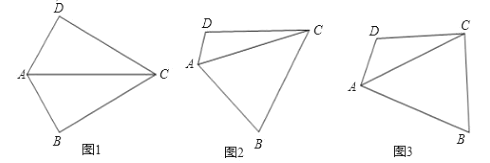
(1)如图1,若![]() ,且
,且![]() ,直接写出线段
,直接写出线段![]() 、
、![]() 、
、![]() 的数量关系.
的数量关系.
(2)如图2,若将(1)中的条件“![]() ”去掉,求边
”去掉,求边![]() 、
、![]() 与对角线
与对角线![]() 的数量关系.请证明.
的数量关系.请证明.
(3)如图3,若![]() ,直接写出边
,直接写出边![]() 、
、![]() 与对角线
与对角线![]() 的数量关系(用
的数量关系(用![]() 来表示)
来表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
a.国家创新指数得分的频数分布直方图(数据分成7组:
30≤x<40,40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
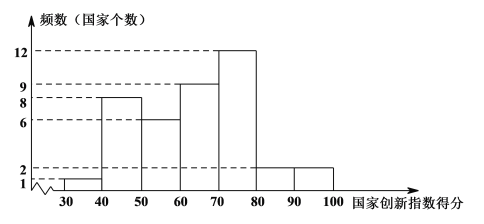
b.国家创新指数得分在60≤x<70这一组的是:61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5
c.40个国家的人均国内生产总值和国家创新指数得分情况统计图:
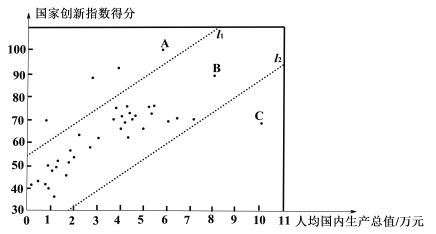
d.中国的国家创新指数得分为69.5.
(以上数据来源于《国家创新指数报告(2018)》)
根据以上信息,回答下列问题:
(1)中国的国家创新指数得分排名世界第______;
(2)在40个国家的人均国内生产总值和国家创新指数得分情况统计图中,包括中国在内的少数几个国家所对应的点位于虚线![]() 的上方.请在图中用“
的上方.请在图中用“![]() ”圈出代表中国的点;
”圈出代表中国的点;
(3)在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为______万美元;(结果保留一位小数)
(4)下列推断合理的是______.
①相比于点A,B所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;
②相比于点B,C所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com