
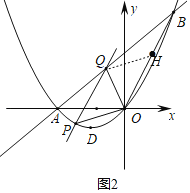
【题目】如图,抛物线y=ax2+bx(a≠0)与x轴交于原点及点A,且经过点B(4,8),对称轴为直线x=﹣2,顶点为D.
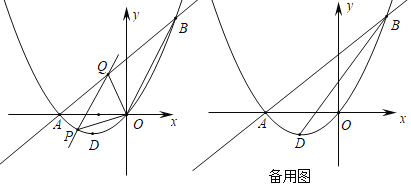
(1)填空:抛物线的解析式为 ,顶点D的坐标为 ,直线AB的解析式为 ;
(2)在直线AB左侧抛物线上存在点E,使得∠EBA=∠ABD,求E的坐标;
(3)连接OB,点P为x轴下方抛物线上一动点,过点P作OB的平行线交直线AB于点Q,当S△POQ:S△BOQ=1:2时,求出点P的坐标.
【答案】(1)y=![]() x2+x;(﹣2,﹣1);y=x+4;(2)(﹣
x2+x;(﹣2,﹣1);y=x+4;(2)(﹣![]() ,
,![]() );(3)P(﹣2
);(3)P(﹣2![]() ,2﹣2
,2﹣2![]() ).
).
【解析】
(1)根据对称轴可求得A点坐标,再根据B点坐标,利用待定系数法即可求得抛物线以及一次函数解析式,再利用对称轴为x=﹣2可求得抛物线顶点坐标;
(2)证明四边形GDHD′为正方形,点D(-2,-1),则点G(-5,-1),则正方形的边长为3,则点D′(-5,2),求得直线BD′的解析式,与抛物线联立即可求解;
(3)证明四边形PQHO为平行四边形,则xQ-xP=xH-xO,即可求解.
解:(1)对称轴为直线x=﹣2,则点A(﹣4,0),
将点A、B的坐标代入抛物线表达式得![]() ,解得
,解得![]() .
.
故抛物线的表达式为:y=![]() x2+x…①,
x2+x…①,
当x=-2时,![]()
∴顶点D的坐标为:(﹣2,﹣1),
设直线AB的表达式为![]() ,
,
将点A、B的坐标代入一次函数表达式![]() ,解得
,解得![]() ,
,
所以,直线AB的表达式为:y=x+4…②,
故答案为:y=![]() x2+x;(﹣2,﹣1);y=x+4;
x2+x;(﹣2,﹣1);y=x+4;
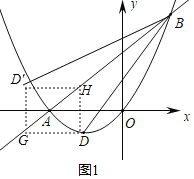
(2)作点D关于AB的对称点D′,分别过点D、D′作x轴的平行线交直线AB与点G、H,
则![]() ,
,![]() ,
,
∵直线AB的解析式为y=x+4,![]() ∥x轴,
∥x轴,![]() ∥x轴,
∥x轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
则四边形GDHD′为正方形,
根据点D(﹣2,﹣1),可得点G(﹣5,﹣1),
所以,正方形的边长为3,
则点D′(﹣5,2),
设直线BD′的表达式为:![]() ,所以
,所以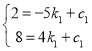 ,解得
,解得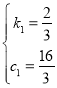 ,
,
所以,直线BD′的表达式为:y=![]() x+
x+![]() …③;
…③;
联立①③并解得:x=﹣![]() 或4(舍去),
或4(舍去),
故点E(﹣![]() ,
,![]() );
);
(3)取OB的中点H(2,4),则S△OQH=![]() S△OBQ,而S△POQ:S△BOQ=1:2,
S△OBQ,而S△POQ:S△BOQ=1:2,
故S△OQH=S△POQ,
∵PQ∥OH,故PQ=OH(四边形PQHO为平行四边形),
则xQ﹣xP=xH﹣xO,
设点P(m,![]() m2+m),
m2+m),
直线OB的表达式为:y=2x,
则直线PQ的表达式为:y=2x+b1,将点P的坐标代入上式得![]() ,解得
,解得![]() ,
,
所以,直线PQ的表达式为:y=2x+![]() m2﹣m…④,
m2﹣m…④,
联立②④并解得:xQ=﹣![]() m2+m+4,
m2+m+4,
而xQ﹣xP=xH﹣xO,
即﹣![]() m2+m+4﹣m=2,
m2+m+4﹣m=2,
解得:m=![]() 或m=
或m=![]() (舍去),
(舍去),
故点P(﹣2![]() ,2﹣2
,2﹣2![]() ).
).


科目:初中数学 来源: 题型:
【题目】某学校为了创建书香校园,去年购买了一批图书.其中科普书的单价比文学书的单价多8元,用1800元购买的科普书的数量与用l000元购买的文学书的数量相同.
(1)求去年购买的文学书和科普书的单价各是多少元;
(2)这所学校今年计划再购买这两种文学书和科普书共200本,且购买文学书和科普书的总费用不超过2088元.今年文学书的单价比去年提高了20%,科普书的单价与去年相同,且每购买1本科普书就免费赠送1本文学书,求这所学校今年至少要购买多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
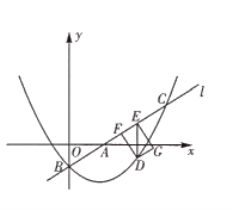
【题目】如图,已知直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() 抛物线
抛物线![]() 经过点
经过点![]() 与直线
与直线![]() 的另一个交点为
的另一个交点为![]() .
.
![]() 求
求![]() 的值和抛物线的解析式
的值和抛物线的解析式
![]() 点
点![]() 在抛物线上,
在抛物线上,![]() 轴交直线
轴交直线![]() 于点
于点![]() 点
点![]() 在直线
在直线![]() 上,且四边形
上,且四边形![]() 为矩形.设点
为矩形.设点![]() 的横坐标为
的横坐标为![]() 矩形
矩形![]() 的周长为
的周长为![]() 求
求![]() 与
与![]() 的函数关系式以及
的函数关系式以及![]() 的最大值
的最大值
![]() 将
将![]() 绕平面内某点
绕平面内某点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() (点
(点![]() 分别与
分别与![]() 点对应),若
点对应),若![]() 的两个顶点恰好落在抛物线上,请直接写出点
的两个顶点恰好落在抛物线上,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月10日傍晚18:10左右,江苏省无锡市山区312国道上海方向K135处,锡港路上跨桥出现桥面侧翻,造成3人死亡,2人受伤,尽管该事故原因初步分析为半挂牵引车严重超载导致桥梁发生侧翻,但是也引起了社会各界对桥梁设计安全性的担忧,我市积极开展对桥梁结构设计的安全性进行评估(已知:抗倾覆系数越高,安全性越强;当抗倾覆系数≥2.5时,认为该结构安全),现在重庆市随机抽取了甲、乙两个设计院,对其各自在建的或已建的20座桥梁项目进行排查,将得到的抗倾覆数据进行整理、描述和分析(抗倾覆数据用x表示,共分成6组:A.0≤x<2.5,B.2.5≤x<5.0,C.5.0≤x<7.5,D.7.5≤x<10.0,E.10.0≤x<12.5,F.12.5≤x<15),下面给出了部分信息;
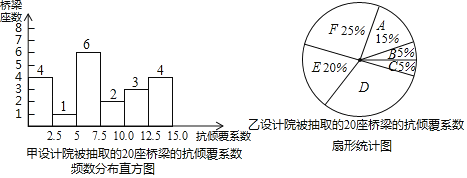
其中,甲设计院C组的抗倾覆系数是:7,7,7,6,7,7;
乙设计院D组的抗倾覆系数是:8,8,9,8,8,8;
甲、乙设计院分别被抽取的20座桥梁的抗倾覆系数统计表
设计院 | 甲 | 乙 |
平均数 | 7.7 | 8.9 |
众数 | a | 8 |
中位数 | 7 | b |
方差 | 19.7 | 18.3 |
根据以上信息解答下列问题:
(1)扇形统计图中D组数据所对应的圆心角是 度,a= ,b= ;
(2)根据以上数据,甲、乙两个设计院中哪个设计院的桥梁安全性更高,说明理由(一条即可): ;
(3)据统计,2018年至2019年,甲设计院完成设计80座桥梁,乙设计院完成设计120座桥梁,请估算2018年至2019年两设计院的不安全桥梁的总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以矩形ABCD对角线AC为底边作等腰直角△ACE,连接BE,分别交AD,AC于点F,N,CD=AF,AM平分∠BAN.下列结论:①EF⊥ED;②∠BCM=∠NCM;③AC=![]() EM;④BN2+EF2=EN2;⑤AEAM=NEFM,其中正确结论的个数是( )
EM;④BN2+EF2=EN2;⑤AEAM=NEFM,其中正确结论的个数是( )
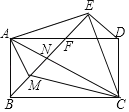
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”
请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
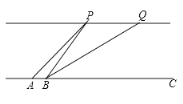
【题目】如图,![]() 、
、![]() 为河对岸的两幢建筑物,某学习小组为了测出河宽(沿岸是平行的),先在岸边的点
为河对岸的两幢建筑物,某学习小组为了测出河宽(沿岸是平行的),先在岸边的点![]() 处测得
处测得![]() ,再沿着河岸前进10米后到达
,再沿着河岸前进10米后到达![]() 点,在点
点,在点![]() 处测得
处测得![]() ,
,![]() .
.
(1)求河宽;
(2)该小组发现此时还可求得![]() 、
、![]() 之间的距离,请求出
之间的距离,请求出![]() 的长.(精确到0.1米)(参考数据:
的长.(精确到0.1米)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
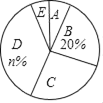
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)郑州市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com