
【题目】2019年10月10日傍晚18:10左右,江苏省无锡市山区312国道上海方向K135处,锡港路上跨桥出现桥面侧翻,造成3人死亡,2人受伤,尽管该事故原因初步分析为半挂牵引车严重超载导致桥梁发生侧翻,但是也引起了社会各界对桥梁设计安全性的担忧,我市积极开展对桥梁结构设计的安全性进行评估(已知:抗倾覆系数越高,安全性越强;当抗倾覆系数≥2.5时,认为该结构安全),现在重庆市随机抽取了甲、乙两个设计院,对其各自在建的或已建的20座桥梁项目进行排查,将得到的抗倾覆数据进行整理、描述和分析(抗倾覆数据用x表示,共分成6组:A.0≤x<2.5,B.2.5≤x<5.0,C.5.0≤x<7.5,D.7.5≤x<10.0,E.10.0≤x<12.5,F.12.5≤x<15),下面给出了部分信息;
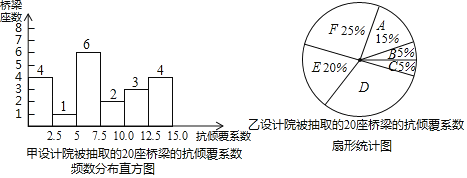
其中,甲设计院C组的抗倾覆系数是:7,7,7,6,7,7;
乙设计院D组的抗倾覆系数是:8,8,9,8,8,8;
甲、乙设计院分别被抽取的20座桥梁的抗倾覆系数统计表
设计院 | 甲 | 乙 |
平均数 | 7.7 | 8.9 |
众数 | a | 8 |
中位数 | 7 | b |
方差 | 19.7 | 18.3 |
根据以上信息解答下列问题:
(1)扇形统计图中D组数据所对应的圆心角是 度,a= ,b= ;
(2)根据以上数据,甲、乙两个设计院中哪个设计院的桥梁安全性更高,说明理由(一条即可): ;
(3)据统计,2018年至2019年,甲设计院完成设计80座桥梁,乙设计院完成设计120座桥梁,请估算2018年至2019年两设计院的不安全桥梁的总数.
【答案】(1)108,7,8.5;(2)乙设计院的平均数和众数都高于甲设计院;(3)2018年至2019年两设计院的不安全桥梁的一共有34座.
【解析】
(1)根据扇形统计图中的数据可以计算出扇形统计图中D组数据所对应的圆心角,再根据题目中给出的数据可以得到a、b的值;
(2)根据题目中的数据,可以判断出甲、乙两个设计院中哪个设计院的桥梁安全性更高,然后说出一条理由即可,注意理由的答案不唯一,只要合理即可;
(3)根据题目中的数据可以计算出2018年至2019年两设计院的不安全桥梁的总数.
解:(1)扇形统计图中D组数据所对应的圆心角是:360°×(1﹣15%﹣5%﹣5%﹣20%﹣25%)=108°,
a=7,
20×(25%+20%)=9,则乙组第10个数据和第11个数据是8,9,故b=(8+9)÷2=8.5,
故答案为:108,7,8.5;
(2)根据以上数据,甲、乙两个设计院中乙设计院的桥梁安全性更高,理由是乙设计院的平均数和众数都高于甲设计院,
故答案为:乙设计院的平均数和众数都高于甲设计院;
(3)80×![]() +120×15%
+120×15%
=16+18
=34(座),
答:2018年至2019年两设计院的不安全桥梁的一共有34座.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
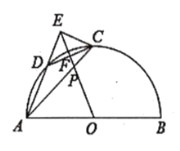
【题目】如图,在以![]() 为直径的半
为直径的半![]() 上有
上有![]() C,点
C,点![]() 在
在![]() 上,过圆心
上,过圆心![]() 作
作![]() 的于点
的于点![]() 的延长线交于点
的延长线交于点![]() ,连结
,连结![]() ,若
,若![]() .
.
![]() 试说明
试说明![]() ;
;
![]() 若
若![]() 的面积为
的面积为![]() 面积的
面积的![]() 倍,连接
倍,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值和
的值和![]() 的长:
的长:
![]() 在
在![]() 的条件下,延长
的条件下,延长![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,直接写
,直接写![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
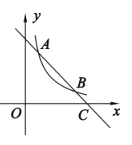
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象在第一象限交于
的图象在第一象限交于![]() 两点,一次函数的图象与
两点,一次函数的图象与![]() 轴交于点
轴交于点![]() .
.
(1)求反比例函数和一次函数的表达式;
(2)当![]() 为何值时,
为何值时,![]() ?
?
(3)已知点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,在第一象限内交一次函数
轴的平行线,在第一象限内交一次函数![]() 的图象于点
的图象于点![]() ,交反比例函数
,交反比例函数![]() 的图象于点
的图象于点![]() .结合函数图象直接写出当
.结合函数图象直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一条道路上,甲车从![]() 地到
地到![]() 地,乙车从
地,乙车从![]() 地到
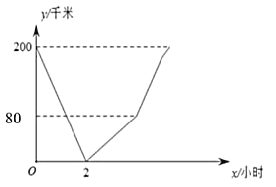
地到![]() 地,两车同时出发以各自速度匀速行驶. 两车相遇后,乙车休息了
地,两车同时出发以各自速度匀速行驶. 两车相遇后,乙车休息了![]() 小时,然后继续原速驶往
小时,然后继续原速驶往![]() 地,图中的折线段表示甲、乙两车之间的距离
地,图中的折线段表示甲、乙两车之间的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)的函数关系的图象,下列说法错误的是( )
(小时)的函数关系的图象,下列说法错误的是( )
A.甲乙两车出发![]() 小时后相遇B.甲车速度是
小时后相遇B.甲车速度是![]() 千米/小时
千米/小时
C.甲车到![]() 地比乙车到
地比乙车到![]() 地早
地早![]() D.相遇时乙车距离
D.相遇时乙车距离![]() 地
地![]() 千米
千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
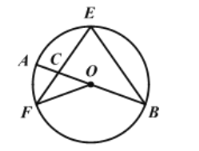
A.20°B.35°C.40°D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a≠0)与x轴交于原点及点A,且经过点B(4,8),对称轴为直线x=﹣2,顶点为D.
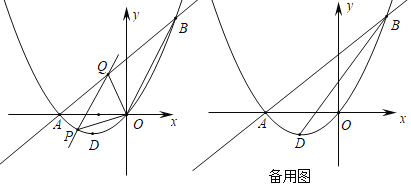
(1)填空:抛物线的解析式为 ,顶点D的坐标为 ,直线AB的解析式为 ;
(2)在直线AB左侧抛物线上存在点E,使得∠EBA=∠ABD,求E的坐标;
(3)连接OB,点P为x轴下方抛物线上一动点,过点P作OB的平行线交直线AB于点Q,当S△POQ:S△BOQ=1:2时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“过圆外一点作圆的切线”的尺规作图的过程.
已知:如图1,![]() 和
和![]() 外的一点
外的一点![]() .
.
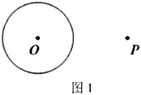
求作:过点![]() 作
作![]() 的切线.
的切线.
作法:如图2,
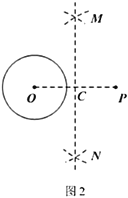
①连接![]() ;
;
②作线段![]() 的垂直平分线
的垂直平分线![]() ,直线
,直线![]() 交
交![]() 于
于![]() ;
;
③以点![]() 为圆心,
为圆心,![]() 为半径作圆,交
为半径作圆,交![]() 于点
于点![]() 和
和![]() ;
;
④作直线![]() 和
和![]() .
.
则![]() ,
,![]() 就是所求作的
就是所求作的![]() 的切线.
的切线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:连接![]() ,
,![]() ,
,
∵由作图可知![]() 是
是![]() 的直径,
的直径,
∴![]() (______)(填依据),
(______)(填依据),
∴![]() ,
,![]() ,
,
又∵![]() 和
和![]() 是
是![]() 的半径,
的半径,
∴![]() ,
,![]() 就是
就是![]() 的切线(______)(填依据).
的切线(______)(填依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]() (k是常数).
(k是常数).
(1)若该函数的图象与x轴有两个不同的交点,试求k的取值范围;
(2)若点(1,k)在某反比例函数图象上,要使该反比例函数和二次函数y=![]() 都是y随x的增大而增大,求k应满足的条件及x的取值范围;
都是y随x的增大而增大,求k应满足的条件及x的取值范围;
(3)若抛物线y=![]() 与x轴交于A(
与x轴交于A(![]() ,0)、B(
,0)、B(![]() ,0)两点,且
,0)两点,且![]() <
<![]() ,
,![]() =34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于
=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )两点,试探究
)两点,试探究![]() 是否为定值,并写出探究过程.
是否为定值,并写出探究过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com