
【题目】如图,Rt△ABC中,BC=AC=2,D是斜边AB上一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D平行于Rt△ABC的直角边时,AD的长为 . 
【答案】2或2 ![]() ﹣2
﹣2
【解析】解:Rt△ABC中,BC=AC=2, ∴AB=2 ![]() ,∠B=∠A′CB=45°,
,∠B=∠A′CB=45°,
①如图1,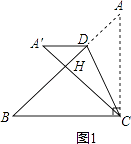
当A′D∥BC,设AD=x,
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴∠A′=∠A=∠A′CB=45°,A′D=AD=x,
∵∠B=45°,
∴A′C⊥AB,
∴BH= ![]() BC=
BC= ![]() ,DH=
,DH= ![]() A′D=
A′D= ![]() x,
x,
∴x ![]() +
+ ![]() =2
=2 ![]() ,
,
∴x=2 ![]() ﹣2,
﹣2,
∴AD=2 ![]() ﹣2;
﹣2;
②如图2,当A′D∥AC,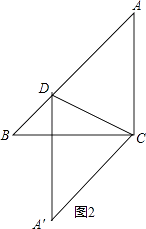
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴AD=A′D,AC=A′C,∠ACD=∠A′CD,
∵∠A′DC=∠ACD,
∴∠A′DC=∠A′CD,
∴A′D=A′C,
∴AD=AC=2,
综上所述:AD的长为:2或2 ![]() ﹣2.
﹣2.
在Rt△ABC中,BC=AC=2,于是得到AB=2 ![]() ,∠B=∠A′CB=45°,①如图1,当A′D∥BC,设AD=x,根据折叠的性质得到∠A′=∠A=∠A′CB=45°,A′D=AD=x,推出A′C⊥AB,求得BH=
,∠B=∠A′CB=45°,①如图1,当A′D∥BC,设AD=x,根据折叠的性质得到∠A′=∠A=∠A′CB=45°,A′D=AD=x,推出A′C⊥AB,求得BH= ![]() BC=
BC= ![]() ,DH=
,DH= ![]() A′D=
A′D= ![]() x,然后列方程即可得到结果,②如图2,当A′D∥AC,根据折叠的性质得到AD=A′D,AC=A′C,∠ACD=∠A′CD,根据平行线的性质得到∠A′DC=∠ACD,于是得到∠A′DC=∠A′CD,推出A′D=A′C,于是得到AD=AC=2.
x,然后列方程即可得到结果,②如图2,当A′D∥AC,根据折叠的性质得到AD=A′D,AC=A′C,∠ACD=∠A′CD,根据平行线的性质得到∠A′DC=∠ACD,于是得到∠A′DC=∠A′CD,推出A′D=A′C,于是得到AD=AC=2.


科目:初中数学 来源: 题型:
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考前各校初三学生都要进行体育测试,某次中考体育测试设有A、B两处考点,甲、乙、丙三名学生各自随机选择其中的一处进行中考体育测试,请用表格或树状图分析:
(1)求甲、乙、丙三名学生在同一处进行体育测试的概率;
(2)求甲、乙、丙三名学生中至少有两人在B处进行体育测试的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一直角坐标系中,直线y=﹣x+3与y=3x﹣5相交于C点,分别与x轴交于A、B两点.P、Q分别为直线y=﹣x+3与y=3x﹣5上的点.
(1)求△ABC的面积;
(2)若P、Q关于原点成中心对称,求P点的坐标;
(3)若△QPC≌△ABC,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,圆规两脚形成的角α称为圆规的张角.一个圆规两脚均为12cm,最大张角150°,你能否画出一个半径为20cm的圆?请借助图2说明理由.(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+bx+c的图象经过坐标原点,与x轴交于点A(﹣2,0). 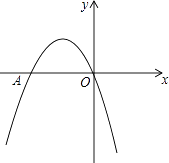
(1)求此二次函数的解析式;
(2)在抛物线上有一点P,满足S△AOP=1,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+bx+c的图象经过坐标原点,与x轴交于点A(﹣2,0). 
(1)求此二次函数的解析式;
(2)在抛物线上有一点P,满足S△AOP=1,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同,现在两辆汽车经过这个十字路口.
(1)请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;
(2)求这两辆汽车都向左转的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,﹣4).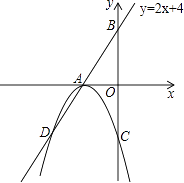
(1)求抛物线的解析式;
(2)将抛物线顶点沿着直线AB平移,此时顶点记为E,与y轴的交点记为F,
①求当△BEF与△BAO相似时,E点坐标;
②记平移后抛物线与AB另一个交点为G,则S△EFG与S△ACD是否存在8倍的关系?若有请直接写出F点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com