
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 延长线上的一点,
延长线上的一点,![]() 交
交![]() 于点
于点![]() ,且
,且![]() .
.
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 请直接写出图中某
请直接写出图中某![]() 条线段之间的等量关系式,只要写出
条线段之间的等量关系式,只要写出![]() 个.(添加的辅助线不能用)
个.(添加的辅助线不能用)
【答案】(1)连结![]() .
.
![]() 是直径,
是直径,![]() .
.
![]() ,
,![]() ,
,![]() 是等边三角形
是等边三角形
而![]() ,
,![]() ,
,
![]() ,
,
即![]() ,故
,故![]() 是⊙O的切线.
是⊙O的切线.
(2)OA=OB=BC=BD
【解析】
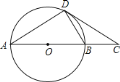
(1)连接OD,由AB为圆O的直径,根据直径所对的圆周角为直角得到∠ADB为直角,再由∠A为30°,利用三角形的内角和定理求出∠OBD为60°,再由OD=OB,得到三角形OBD为等边三角形,根据等边三角形的性质得到内角∠ODB为60°,又∠OBD为三角形BDC的外角,利用外角的性质得到∠BDC=∠OBD-∠C,求出∠BDC为30°,进而确定出∠ODC为直角,即DC垂直于OD,可得出CD为圆O的切线,得证;
(2)由O为AB的中点得到OA=OB,再由三角形ODB为等边三角形可得出DB=OB,在直角三角形OCD中,根据30°角所对的直角边等于斜边的一半得出OD为OC的一半,即OB为OC的一半,即B为OC中点,可得出BC=OB,即可得到OA=OB=BC=BD,找出其中的三条线段相等即可.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究发现)
如图1,在△ABC中,点P是内角∠ABC和外角∠ACD的角平分线的交点,试猜想∠P与∠A之间的数量关系,并证明你的猜想.

(迁移拓展)
如图2,在△ABC中,点P是内角∠ABC和外角∠ACD的n等分线的交点,即∠PBC=![]() ∠ABC,∠PCD=
∠ABC,∠PCD=![]() ∠ACD,
∠ACD,
试猜想∠P与∠A之间的数量关系,并证明你的猜想.
(应用创新)
已知,如图3,AD、BE相交于点C,∠ABC、∠CDE、∠ACE的角平分线交于点P,∠A=35°,∠E=25°,则∠BPD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
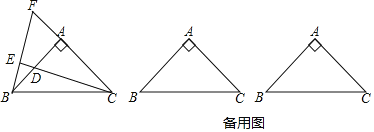
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,证明:AB=FA+BD;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
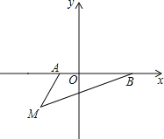
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+2|+(b﹣4)2=0.
(1)填空:a=_____,b=_____;
(2)如果在第三象限内有一点M(﹣3,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=﹣3时,在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
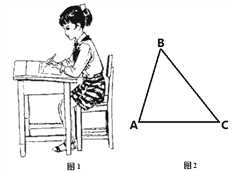
【题目】人写字时眼睛和笔端的距离超过30cm时则符合保护视力的要求.图1是一位同学的坐姿,把她的眼睛B、肘关节C和笔端A的位置关系抽象成图2的△ABC,BC=30cm,AC=22cm,∠ACB=530,她的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin530≈0.8,cos530≈0.6,tan530≈1.3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某货船以![]() 海里/小时的速度将一批重要物资由
海里/小时的速度将一批重要物资由![]() 处运往正西方向的目的地
处运往正西方向的目的地![]() 处,经
处,经![]() 小时的航行到达,到达后必须立即卸货,接到气象部门的通知,一台风中心正以
小时的航行到达,到达后必须立即卸货,接到气象部门的通知,一台风中心正以![]() 海里/小时的速度由
海里/小时的速度由![]() 向北偏西
向北偏西![]() 方向移动,距台风中心
方向移动,距台风中心![]() 海里
海里
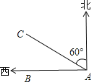
的圆形区域(包括边界)都会受到影响.
(1)![]() 处是否会受到台风的影响答:________(请填“会”或“不会”)
处是否会受到台风的影响答:________(请填“会”或“不会”)
![]() 为避免受到台风的影响,该船应在________小时内卸完货物.(结果保留根号)
为避免受到台风的影响,该船应在________小时内卸完货物.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
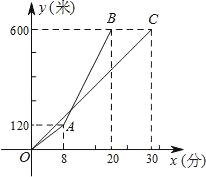
【题目】甲、乙两人沿同一路线登山,图中线段OC、折线OAB分别是甲、乙两人登山的路程y(米)与登山时间x(分)之间的函数图象.请根据图象所提供的信息,解答如下问题:
(1)求甲登山的路程与登山时间之间的函数关系式,并写出自变量x的取值范围;
(2)求乙出发后多长时间追上甲?此时乙所走的路程是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
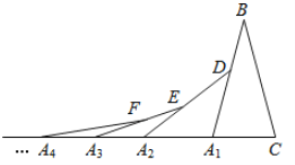
【题目】如图,在第1个![]() 中,
中,![]() ,
,![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,得到第2个
,得到第2个![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .得到第3个
.得到第3个![]() ...按此做法继续下去,则第
...按此做法继续下去,则第![]() 个三角形中以
个三角形中以![]() 为顶点的内角度数是( )
为顶点的内角度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com