
【题目】随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.
(1)该市的养老床位数从![]() 年底的
年底的![]() 万个增长到
万个增长到![]() 年底的
年底的![]() 万个,求该市这两年(从
万个,求该市这两年(从![]() 年底到
年底到![]() 年底)拥有的养老床位数的平均年增长率;
年底)拥有的养老床位数的平均年增长率;
(2)若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共![]() 间,这三类养老专用房间分别为单人间(
间,这三类养老专用房间分别为单人间(![]() 个养老床位),双人间(
个养老床位),双人间(![]() 个养老床位),三人间(
个养老床位),三人间(![]() 个养老床位),因实际需要,单人间房间数在
个养老床位),因实际需要,单人间房间数在![]() 至
至![]() 之间(包括
之间(包括![]() 和
和![]() ),且双人间的房间数是单人间的
),且双人间的房间数是单人间的![]() 倍,设规划建造单人间的房间数为
倍,设规划建造单人间的房间数为![]() .
.
①若该养老中心建成后可提供养老床位![]() 个,求
个,求![]() 的值;
的值;
②直接写出:该养老中心建成后最多提供养老床位 个;最少提供养老床位 个.
【答案】(1)该市这两年拥有的养老床位数的平均年增长率为![]() ;(2)①
;(2)①![]() 的值是
的值是![]() ;②
;②![]() ,
,![]() .
.
【解析】
(1)设该市这两年拥有的养老床位数的平均年增长率为x,根据“2016年的床位数=2014年的床位数×(1+增长率)的平方”可列出关于x的一元二次方程,解方程即可得出结论;
(2)①设规划建造单人间的房间数为t(10≤t≤30),则建造双人间的房间数为2t,三人间的房间数为100﹣3t,根据“可提供的床位数=单人间数+2倍的双人间数+3倍的三人间数”即可得出关于t的一元一次方程,解方程即可得出结论;
②设该养老中心建成后能提供养老床位y个,根据“可提供的床位数=单人间数+2倍的双人间数+3倍的三人间数”即可得出y关于t的函数关系式,根据一次函数的性质结合t的取值范围,即可得出结论.
(1)设该市这两年拥有的养老床位数的平均年增长率为x,由题意可列出方程:
2(1+x)2=2.88
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:该市这两年拥有的养老床位数的平均年增长率为20%.
(2)①设规划建造单人间的房间数为t(10≤t≤30),则建造双人间的房间数为2t,三人间的房间数为100﹣3t,由题意得:t+4t+3(100﹣3t)=200,解得:t=25.
答:t的值是25.
②设该养老中心建成后能提供养老床位y个,由题意得:y=t+4t+3(100﹣3t)=﹣4t+300(10≤t≤30).
∵k=﹣4<0,∴y随t的增大而减小.
当t=10时,y的最大值为300﹣4×10=260(个),当t=30时,y的最小值为300﹣4×30=180(个).
答:该养老中心建成后最多提供养老床位260个,最少提供养老床位180个.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=45°,CD=![]() ,BC=
,BC=![]() ,连接AC、BD,若AC⊥AB,则BD的长度为_______________.
,连接AC、BD,若AC⊥AB,则BD的长度为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校20名数学教师的年龄(单位:岁)情况如下:29,42,58,37,53,52,49,24,37,46,42,55,40,38,50,26,54,26,44,52.
(1)填写下面的频率分布表:
分组 | 频数 | 频率 |
19.5~29.5 | ||
29.5~39.5 | ||
39.5~49.5 | ||
49.5~59.5 | ||
合计 |
(2)画出数据的频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个警察抓两个小偷,目击者说:两个小偷分别躲藏在六个房间中的两间,但不知道他们到底躲藏在哪两间。而如果警察冲进了无人的房间,那么小偷就会趁机逃跑。如果两个警察随机地冲进两个房间抓小偷,(1)至少能抓获一个小偷的概率是多少?(2)两个小偷全部抓获的概率是多少?请简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E为边AD的中点,且∠ABC=60°,AB=6,BE交AC于点F,则AF=( )
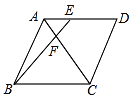
A. 1 B. 2 C. 2.5 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
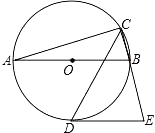
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
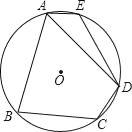
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在![]() 上.
上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=90°,AB=AC=4,D是BC边上一点,将点D绕点A逆时针旋转60°得到点E,连接CE.
![]()

(1)当点E在BC边上时,画出图形并求出∠BAD的度数;
(2)当△CDE为等腰三角形时,求∠BAD的度数;
(3)在点D的运动过程中,求CE的最小值.
(参考数值:sin75°=![]() , cos75°=
, cos75°=![]() ,tan75°=
,tan75°=![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com