
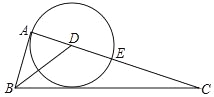
【题目】如图,△ABC中,∠A=90°,AB=AC=4,D是BC边上一点,将点D绕点A逆时针旋转60°得到点E,连接CE.
![]()

(1)当点E在BC边上时,画出图形并求出∠BAD的度数;
(2)当△CDE为等腰三角形时,求∠BAD的度数;
(3)在点D的运动过程中,求CE的最小值.
(参考数值:sin75°=![]() , cos75°=
, cos75°=![]() ,tan75°=
,tan75°=![]() )
)
【答案】(1)∠BAD=15°;(2)∠BAC=45°或∠BAD =60°;(3)CE=![]() .
.
【解析】
(1)如图1中,当点E在BC上时.只要证明△BAD≌△CAE,即可推出∠BAD=∠CAE=![]() (90°-60°)=15°;
(90°-60°)=15°;
(2)分两种情形求解①如图2中,当BD=DC时,易知AD=CD=DE,此时△DEC是等腰三角形.②如图3中,当CD=CE时,△DEC是等腰三角形;
(3)如图4中,当E在BC上时,E记为E′,D记为D′,连接EE′.作CM⊥EE′于M,E′N⊥AC于N,DE交AE′于O.首先确定点E的运动轨迹是直线EE′(过点E与BC成60°角的直线上),可得EC的最小值即为线段CM的长(垂线段最短).
解:(1)如图1中,当点E在BC上时.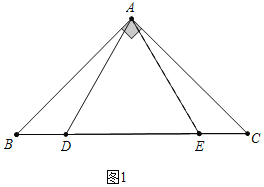
∵AD=AE,∠DAE=60°,
∴△ADE是等边三角形,
∴∠ADE=∠AED=60°,
∴∠ADB=∠AEC=120°,
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
在△ABD和△ACE中,
∠B=∠C,∠ADB=∠AEC,AB=AC,
∴△BAD≌△CAE,
∴∠BAD=∠CAE=![]() (90°-60°)=15°.
(90°-60°)=15°.
(2)①如图2中,当BD=DC时,易知AD=CD=DE,此时△DEC是等腰三角形,∠BAD=![]() ∠BAC=45°.
∠BAC=45°.
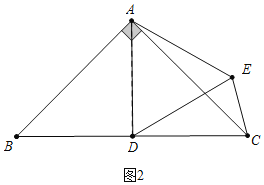
②如图3中,当CD=CE时,△DEC是等腰三角形.
∵AD=AE,
∴AC垂直平分线段DE,
∴∠ACD=∠ACE=45°,
∴∠DCE=90°,
∴∠EDC=∠CED=45°,
∵∠B=45°,
∴∠EDC=∠B,
∴DE∥AB,
∴∠BAD=∠ADE=60°.
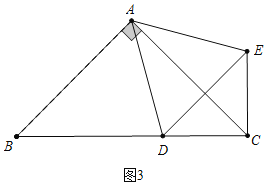
(3)如图4中,当E在BC上时,E记为E′,D记为D′,连接EE′.作CM⊥EE′于M,E′N⊥AC于N,DE交AE′于O.
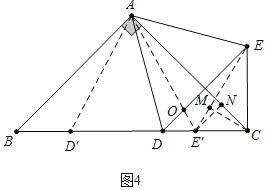
∵∠AOE=∠DOE′,∠AE′D=∠AEO,
∴△AOE∽△DOE′,
∴AO:OD=EO:OE',
∴AO:EO=OD:OE',
∵∠AOD=∠EOE′,
∴△AOD∽△EOE′,
∴∠EE′O=∠ADO=60°,
∴点E的运动轨迹是直线EE′(过点E与BC成60°角的直线上),
∴EC的最小值即为线段CM的长(垂线段最短),
设E′N=CN=a,则AN=4-a,
在Rt△ANE′中,tan75°=AN:NE',
∴2+![]() =
=![]() ,
,
∴a=2-![]() ,
,
∴CE′=![]() CN=2
CN=2![]() -
-![]() .
.
在Rt△CE′M中,CM=CE′cos30°=![]() ,
,
∴CE的最小值为![]() .
.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.
(1)该市的养老床位数从![]() 年底的
年底的![]() 万个增长到
万个增长到![]() 年底的
年底的![]() 万个,求该市这两年(从
万个,求该市这两年(从![]() 年底到
年底到![]() 年底)拥有的养老床位数的平均年增长率;
年底)拥有的养老床位数的平均年增长率;
(2)若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共![]() 间,这三类养老专用房间分别为单人间(
间,这三类养老专用房间分别为单人间(![]() 个养老床位),双人间(
个养老床位),双人间(![]() 个养老床位),三人间(
个养老床位),三人间(![]() 个养老床位),因实际需要,单人间房间数在
个养老床位),因实际需要,单人间房间数在![]() 至
至![]() 之间(包括
之间(包括![]() 和
和![]() ),且双人间的房间数是单人间的
),且双人间的房间数是单人间的![]() 倍,设规划建造单人间的房间数为
倍,设规划建造单人间的房间数为![]() .
.
①若该养老中心建成后可提供养老床位![]() 个,求
个,求![]() 的值;
的值;
②直接写出:该养老中心建成后最多提供养老床位 个;最少提供养老床位 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的图象经过A(0,4),B(2,0),C(-2,0)三点.
(1)求二次函数的表达式;
(2)在x轴上有一点D(-4,0),将二次函数的图象沿射线DA方向平移,使图象再次经过点B.
①求平移后图象顶点E的坐标;
②直接写出此二次函数的图象在A,B两点之间(含A,B两点)的曲线部分在平移过程中所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
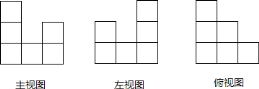
【题目】下面是由些棱长![]() 的正方体小木块搭建成的几何体的主视图、俯视图和左视图,①请你观察它是由多少块小木块组成的;②在俯视图中标出相应位置立方体的个数;③求出该几何体的表面积(包含底面).
的正方体小木块搭建成的几何体的主视图、俯视图和左视图,①请你观察它是由多少块小木块组成的;②在俯视图中标出相应位置立方体的个数;③求出该几何体的表面积(包含底面).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2﹣2x﹣3的图象与x轴的交点为(﹣1,0)和(3,0),交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解.
根据以上方程与函数的关系,如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标,即可知方程x3+2x2﹣x﹣2=0的解.
佳佳为了解函数y=x3+2x2﹣x﹣2的图象,通过描点法画出函数的图象.
x | … | ﹣3 | ﹣ | ﹣2 | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| 2 | … |
y | … | ﹣8 | ﹣ | 0 |
| m | ﹣ | ﹣2 | ﹣ | 0 |
| 12 | … |
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有 个,分别为 ;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
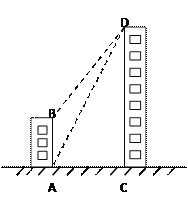
【题目】如图,一栋居民楼AB的高为16米,远处有一栋商务楼CD,小明在居民楼的楼底A处测得商务楼顶D处的仰角为![]() ,又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为
,又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为![]() .其中A、C两点分别位于B、D两点的正下方,且A、C两点在同一水平线上,求商务楼CD的高度.
.其中A、C两点分别位于B、D两点的正下方,且A、C两点在同一水平线上,求商务楼CD的高度.
(参考数据: ![]() ,
, ![]() .结果精确到0.1米)
.结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个200人到300人之间的旅行团队准备外出旅游,旅行团队向某汽车运输公司租用可以乘坐30人、乘坐45人的两种客车若干辆,其中大型客车辆数要多于中型客车辆数.按照预定的租车方案,如果大型客车都坐满,中型客车有一辆就会空出少于一半的座位.但是汽车运输公司发过来的车辆,车型与对应的辆数刚好搞反了,这样就有5个人没有座位可坐.这个旅游团一共有______个人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有小岛A和小岛B,轮船以45km/h的速度由C向B航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈2.45)
≈2.45)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,BD是角平分线,以点D为圆心,DA为半径的⊙D与AC相交于点E
(1)求证:BC是⊙D的切线;
(2)若AB=5,BC=13,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com