
ЁОЬтФПЁПМбМбЯђЬНОПвЛдЊШ§ДЮЗНГЬx3+2x2ЉxЉ2=0ЕФНтЕФЧщПіЃЌИљОнвдЭљЕФбЇЯАОбщЃЌЫћЯыЕНСЫЗНГЬгыКЏЪ§ЕФЙиЯЕЃЌвЛДЮКЏЪ§y=kx+bЃЈkЁй0ЃЉЕФЭМЯѓгыxжсНЛЕуЕФКсзјБъМДЮЊвЛдЊвЛДЮЗНГЬkx+bЃЈkЁй0ЃЉЕФНтЃЌЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгыxжсНЛЕуЕФКсзјБъМДЮЊвЛдЊЖўДЮЗНГЬax2+bx+c=0ЃЈaЁй0ЃЉЕФНтЃЌШчЃКЖўДЮКЏЪ§y=x2Љ2xЉ3ЕФЭМЯѓгыxжсЕФНЛЕуЮЊЃЈЉ1ЃЌ0ЃЉКЭЃЈ3ЃЌ0ЃЉЃЌНЛЕуЕФКсзјБъЉ1КЭ3МДЮЊx2Љ2xЉ3=0ЕФНтЃЎ
ИљОнвдЩЯЗНГЬгыКЏЪ§ЕФЙиЯЕЃЌШчЙћЮвУЧжБЕНКЏЪ§y=x3+2x2ЉxЉ2ЕФЭМЯѓгыxжсНЛЕуЕФКсзјБъЃЌМДПЩжЊЗНГЬx3+2x2ЉxЉ2=0ЕФНтЃЎ
МбМбЮЊСЫНтКЏЪ§y=x3+2x2ЉxЉ2ЕФЭМЯѓЃЌЭЈЙ§УшЕуЗЈЛГіКЏЪ§ЕФЭМЯѓЃЎ
x | Ё | Љ3 | Љ | Љ2 | Љ | Љ1 | Љ | 0 |
| 1 |
| 2 | Ё |
y | Ё | Љ8 | Љ | 0 |
| m | Љ | Љ2 | Љ | 0 |
| 12 | Ё |
ЃЈ1ЃЉжБНгаДГіmЕФжЕЃЌВЂЛГіКЏЪ§ЭМЯѓЃЛ
ЃЈ2ЃЉИљОнБэИёКЭЭМЯѓПЩжЊЃЌЗНГЬЕФНтгаЁЁ ЁЁИіЃЌЗжБ№ЮЊЁЁ ЁЁЃЛ
ЃЈ3ЃЉНшжњКЏЪ§ЕФЭМЯѓЃЌжБНгаДГіВЛЕШЪНx3+2x2ЃОx+2ЕФНтМЏЃЎ
ЁОД№АИЁПЃЈ1ЃЉ0ЃЛЃЈ2ЃЉ3ЃЌЉ2ЃЌЛђЉ1Лђ1ЃЎЃЈ3ЃЉЉ2ЃМxЃМЉ1ЛђxЃО1ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЧѓГіx=Љ1ЪБЕФКЏЪ§жЕМДПЩНтОіЮЪЬтЃЛРћгУУшЕуЗЈЛГіЭМЯѓМДПЩЃЛ
ЃЈ2ЃЉРћгУЭМЯѓвдМАБэИёМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉВЛЕШЪНx3+2x2ЃОx+2ЕФНтМЏЃЌМДЮЊКЏЪ§y=x3+2x2ЉxЉ2ЕФКЏЪ§жЕДѓгк0ЕФздБфСПЕФШЁжЕЗЖЮЇЃЌЙлВьЭМЯѓМДПЩНтОіЮЪЬт.
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЬтвтm=Љ1+2+1Љ2=0ЃЎ
КЏЪ§ЭМЯѓШчЭМЫљЪОЃЎ
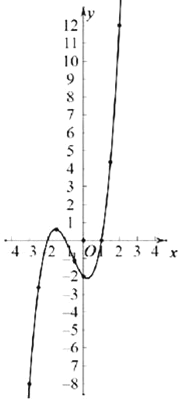
ЃЈ2ЃЉИљОнБэИёКЭЭМЯѓПЩжЊЃЌЗНГЬЕФНтга3ИіЃЌЗжБ№ЮЊЉ2ЃЌЛђЉ1Лђ1ЃЎ
ЃЈ3ЃЉВЛЕШЪНx3+2x2ЃОx+2ЕФНтМЏЃЌМДЮЊКЏЪ§y=x3+2x2ЉxЉ2ЕФКЏЪ§жЕДѓгк0ЕФздБфСПЕФШЁжЕЗЖЮЇЃЎ
ЙлВьЭМЯѓПЩжЊЃЌЉ2ЃМxЃМЉ1ЛђxЃО1ЃЎ


 ЪРМЭАйЭЈЦкФЉН№ОэЯЕСаД№АИ
ЪРМЭАйЭЈЦкФЉН№ОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСНИіОЏВьзЅСНИіаЁЭЕЃЌФПЛїепЫЕЃКСНИіаЁЭЕЗжБ№ЖуВидкСљИіЗПМфжаЕФСНМф,ЕЋВЛжЊЕРЫћУЧЕНЕзЖуВидкФФСНМфЁЃЖјШчЙћОЏВьГхНјСЫЮоШЫЕФЗПМфЃЌФЧУДаЁЭЕОЭЛсГУЛњЬгХмЁЃШчЙћСНИіОЏВьЫцЛњЕиГхНјСНИіЗПМфзЅаЁЭЕЃЌЃЈ1ЃЉжСЩйФмзЅЛёвЛИіаЁЭЕЕФИХТЪЪЧЖрЩйЃПЃЈ2ЃЉСНИіаЁЭЕШЋВПзЅЛёЕФИХТЪЪЧЖрЩйЃПЧыМђЕЅЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггкЁбOЃЌABЃНACЃЌCOЕФбгГЄЯпНЛABгкЕуD.
(1)ЧѓжЄЃКAOЦНЗжЁЯBACЃЛ
(2)ШєBCЃН6ЃЌsinЁЯBACЃН![]() ЃЌЧѓACКЭCDЕФГЄЃЎ
ЃЌЧѓACКЭCDЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§ЕФЭМЯѓЕФЖЅЕудкдЕуOЃЌЧвОЙ§ЕуAЃЈ1ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉЧѓДЫКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉНЋИУХзЮяЯпбизХyжсЯђЩЯЦНвЦКѓЖЅЕуТфдкЕуPДІЃЌжБЯпx=2ЗжБ№НЛдХзЮяКЭаТХзЮяЯпгкЕуMКЭNЃЌЧвSЁїPMN=![]() ЃЌ ЧѓЃКMNЕФГЄвдМАЦНвЦКѓХзЮяЯпЕФНтЮіЪНЃЎ
ЃЌ ЧѓЃКMNЕФГЄвдМАЦНвЦКѓХзЮяЯпЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЮвЙњЕФвЛЫвКЃМрДЌдкЕігуЕКAИННќбие§ЖЋЗНЯђКНааЃЌДЌдкBЕуЪБВтЕУЕігуЕКAдкДЌЕФББЦЋЖЋ60ЁуЗНЯђЃЌДЌвд50КЃРя/ЪБЕФЫйЖШМЬајКНаа2аЁЪБКѓЕНДяCЕуЃЌДЫЪБЕігуЕКAдкДЌЕФББЦЋЖЋ30ЁуЗНЯђЃЎЧыЮЪДЌМЬајКНааЖрЩйКЃРягыЕігуЕКAЕФОрРызюНќЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯA=90ЁуЃЌAB=AC=4ЃЌDЪЧBCБпЩЯвЛЕуЃЌНЋЕуDШЦЕуAФцЪБеыа§зЊ60ЁуЕУЕНЕуEЃЌСЌНгCE.
![]()

(1)ЕБЕуEдкBCБпЩЯЪБ,ЛГіЭМаЮВЂЧѓГіЁЯBADЕФЖШЪ§ЃЛ
(2)ЕБЁїCDEЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЁЯBADЕФЖШЪ§ЃЛ
(3)дкЕуDЕФдЫЖЏЙ§ГЬжаЃЌЧѓCEЕФзюаЁжЕ.
(ВЮПМЪ§жЕ:sin75Ёу=![]() ЃЌ cos75Ёу=
ЃЌ cos75Ёу=![]() ЃЌtan75Ёу=
ЃЌtan75Ёу=![]() )
)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮжНЦЌABCDжаЃЌ ![]() ЃЌНЋСтаЮжНЦЌЗелЃЌЪЙЕуAТфдкCDЕФжаЕуEДІЃЌелКлЮЊFGЃЌЕу
ЃЌНЋСтаЮжНЦЌЗелЃЌЪЙЕуAТфдкCDЕФжаЕуEДІЃЌелКлЮЊFGЃЌЕу![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЩЯЃЌдђ
ЩЯЃЌдђ![]() ЕФжЕЮЊ______ ЃЎ
ЕФжЕЮЊ______ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌAB=CDЃЌDEЁЭACЃЌBFЁЭACЃЌДЙзуЗжБ№ЮЊEЃЌFЃЌЧвDE=BFЃЎЧѓжЄЃК
ЃЈ1ЃЉAE=CFЃЛ
ЃЈ2ЃЉЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМPЮЊЕШБпЁїABCЭтвЛЕуЃЌAHДЙжБЦНЗжPCгкЕуHЃЌЁЯBAPЕФЦНЗжЯпНЛPCгкЕуD
(1) ЧѓжЄЃКDPЃНDB
(2) ЧѓжЄЃКDAЃЋDBЃНDC
(3) ШєЕШБпЁїABCБпГЄЮЊ![]() ЃЌСЌНгBHЃЌЕБЁїBDHЮЊЕШБпШ§НЧаЮЪБЃЌЧыжБНгаДГіCPЕФГЄЖШЮЊ_________
ЃЌСЌНгBHЃЌЕБЁїBDHЮЊЕШБпШ§НЧаЮЪБЃЌЧыжБНгаДГіCPЕФГЄЖШЮЊ_________

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com