练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数的图象的顶点在原点O，且经过点A（1，）．

    （1）求此函数的解析式；

    （2）将该抛物线沿着y轴向上平移后顶点落在点P处，直线x=2分别交原抛物和新抛物线于点M和N，且S△PMN= ， 求：MN的长以及平移后抛物线的解析式．

    【答案】（1）y=x2；（2）3，y=x2+3．

    【解析】

    （1）根据题意可直接设y＝ax2把点（1，﹣3）代入得a＝﹣3，所以y＝﹣3x2；

    （2）设平移后yx2+d（d＞0），则MN＝d，根据题意得出S2×d＝3，即可求得d的值，从而求得平移后的解析式．

    （1）∵抛物线顶点是原点，可设y＝ax2，把点A（1，）代入，得：a＝，所以这个二次函数的关系式为yx2；

    （2）设平移后yx2+d（d＞0），∴MN＝d，S2×d＝3，∴d＝3，∴yx2+3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在△AOB中，C，D分别是OA、OB边上的点，将△OCD绕点O顺时针旋转到△OC′D′．如图，若∠AOB=90°，OA=OB，C，D分别为OA，OB的中点．求证：

    (1)AC′=BD′；

    (2)AC′⊥BD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连结EF、EO，若DE=，∠DPA=45°．

    （1）求⊙O的半径;

    （2）求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，二次函数y＝ax2+bx+c（a≠0）的图象经过A（0，4），B（2，0），C（-2，0）三点．

    （1）求二次函数的表达式；

    （2）在x轴上有一点D（-4，0），将二次函数的图象沿射线DA方向平移，使图象再次经过点B．

    ①求平移后图象顶点E的坐标；

    ②直接写出此二次函数的图象在A，B两点之间（含A，B两点）的曲线部分在平移过程中所扫过的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担．李明按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数:y=-10x+500．

    （1）李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?

    （2）设李明获得的利润为W（元）,当销售单价定为多少元时,每月可获得最大利润?

    （3）物价部门规定,这种节能灯的销售单价不得高于25元．如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

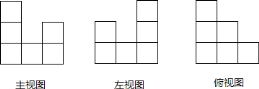
    【题目】下面是由些棱长的正方体小木块搭建成的几何体的主视图、俯视图和左视图，①请你观察它是由多少块小木块组成的；②在俯视图中标出相应位置立方体的个数；③求出该几何体的表面积（包含底面）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况，根据以往的学习经验，他想到了方程与函数的关系，一次函数y=kx+b（k≠0）的图象与x轴交点的横坐标即为一元一次方程kx+b（k≠0）的解，二次函数y=ax2+bx+c（a≠0）的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0（a≠0）的解，如：二次函数y=x2﹣2x﹣3的图象与x轴的交点为（﹣1，0）和（3，0），交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解．

    根据以上方程与函数的关系，如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标，即可知方程x3+2x2﹣x﹣2=0的解．

    佳佳为了解函数y=x3+2x2﹣x﹣2的图象，通过描点法画出函数的图象．

    x

    …

    ﹣3

    ﹣

    ﹣2

    ﹣

    ﹣1

    ﹣

    0

    1

    2

    …

    y

    …

    ﹣8

    ﹣

    0

    m

    ﹣

    ﹣2

    ﹣

    0

    12

    …

    （1）直接写出m的值，并画出函数图象；

    （2）根据表格和图象可知，方程的解有　 　个，分别为　 　；

    （3）借助函数的图象，直接写出不等式x3+2x2＞x+2的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个200人到300人之间的旅行团队准备外出旅游，旅行团队向某汽车运输公司租用可以乘坐30人、乘坐45人的两种客车若干辆，其中大型客车辆数要多于中型客车辆数.按照预定的租车方案，如果大型客车都坐满，中型客车有一辆就会空出少于一半的座位.但是汽车运输公司发过来的车辆，车型与对应的辆数刚好搞反了，这样就有5个人没有座位可坐．这个旅游团一共有______个人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线y=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），有下列结论：①2a+b=0，②abc＞0；③方程ax2+bx+c=3有两个相等的实数根，④当y＜0时，﹣2＜x＜4，其中正确的是（　　）

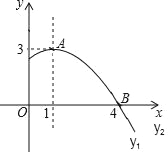
    A. ②③ B. ①③ C. ①③④ D. ①②③④

    查看答案和解析>>

    同步练习册答案