
【题目】在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的图象经过A(0,4),B(2,0),C(-2,0)三点.
(1)求二次函数的表达式;
(2)在x轴上有一点D(-4,0),将二次函数的图象沿射线DA方向平移,使图象再次经过点B.
①求平移后图象顶点E的坐标;
②直接写出此二次函数的图象在A,B两点之间(含A,B两点)的曲线部分在平移过程中所扫过的面积.
【答案】(1)y=﹣x2+4;(2)①E(5,9);②30.
【解析】
(1)待定系数法即可解题,
(2)①求出直线DA的解析式,根据顶点E在直线DA上,设出E的坐标,带入即可求解;②AB扫过的面积是平行四边形ABGE,根据S四边形ABGE=S矩形IOKH﹣S△AOB﹣S△AEI﹣S△EHG﹣S△GBK,求出点B(2,0),G(7,5),A(0,4),E(5,9),根据坐标几何含义即可解题.
解:(1)∵A(0,4),B(2,0),C(﹣2,0)
∴二次函数的图象的顶点为A(0,4),
∴设二次函数表达式为y=ax2+4,
将B(2,0)代入,得4a+4=0,
解得,a=﹣1,
∴二次函数表达式y=﹣x2+4;
(2)①设直线DA:y=kx+b(k≠0),
将A(0,4),D(﹣4,0)代入,得![]() ,
,
解得,![]() ,
,
∴直线DA:y=x+4,
由题意可知,平移后的抛物线的顶点E在直线DA上,
∴设顶点E(m,m+4),
∴平移后的抛物线表达式为y=﹣(x﹣m)2+m+4,
又∵平移后的抛物线过点B(2,0),
∴将其代入得,﹣(2﹣m)2+m+4=0,
解得,m1=5,m2=0(不合题意,舍去),
∴顶点E(5,9),
②如图,连接AB,过点B作BL∥AD交平移后的抛物线于点G,连结EG,

∴四边形ABGE的面积就是图象A,B两点间的部分扫过的面积,
过点G作GK⊥x轴于点K,过点E作EI⊥y轴于点I,直线EI,GK交于点H.
由点A(0,4)平移至点E(5,9),可知点B先向右平移5个单位,再向上平移5个单位至点G.
∵B(2,0),∴点G(7,5),
∴GK=5,OB=2,OK=7,
∴BK=OK﹣OB=7﹣2=5,
∵A(0,4),E(5,9),
∴AI=9﹣4=5,EI=5,
∴EH=7﹣5=2,HG=9﹣5=4,
∴S四边形ABGE=S矩形IOKH﹣S△AOB﹣S△AEI﹣S△EHG﹣S△GBK
=7×9﹣![]() ×2×4﹣
×2×4﹣![]() ×5×5﹣
×5×5﹣![]() ×2×4﹣
×2×4﹣![]() ×5×5
×5×5
=63﹣8﹣25
=30
答:图象A,B两点间的部分扫过的面积为30.


科目:初中数学 来源: 题型:
【题目】某学校20名数学教师的年龄(单位:岁)情况如下:29,42,58,37,53,52,49,24,37,46,42,55,40,38,50,26,54,26,44,52.
(1)填写下面的频率分布表:
分组 | 频数 | 频率 |
19.5~29.5 | ||
29.5~39.5 | ||
39.5~49.5 | ||
49.5~59.5 | ||
合计 |
(2)画出数据的频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
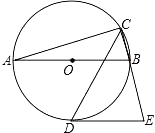
【题目】如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
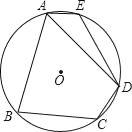
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在![]() 上.
上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D.
(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=![]() ,求AC和CD的长.
,求AC和CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象的顶点在原点O,且经过点A(1,![]() ).
).
(1)求此函数的解析式;
(2)将该抛物线沿着y轴向上平移后顶点落在点P处,直线x=2分别交原抛物和新抛物线于点M和N,且S△PMN=![]() , 求:MN的长以及平移后抛物线的解析式.
, 求:MN的长以及平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=90°,AB=AC=4,D是BC边上一点,将点D绕点A逆时针旋转60°得到点E,连接CE.
![]()

(1)当点E在BC边上时,画出图形并求出∠BAD的度数;
(2)当△CDE为等腰三角形时,求∠BAD的度数;
(3)在点D的运动过程中,求CE的最小值.
(参考数值:sin75°=![]() , cos75°=
, cos75°=![]() ,tan75°=
,tan75°=![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com