
【题目】如图,把三角形纸片![]() 折叠,使
折叠,使![]() 的对应点
的对应点![]() 在
在![]() 上,点
上,点![]() 的对应点
的对应点![]() 在
在![]() 上,折痕分别为
上,折痕分别为![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的长为__________.
的长为__________.
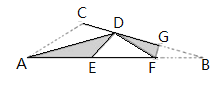
【答案】![]()
【解析】
如图,作DH⊥AB于H,在AH上取一点M,使得AM=DM,连接DM.想办法求出AH,EH即可解决问题.
解:如图,作DH⊥AB交AB于点H.
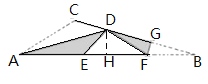
∵∠CAB=30°,∠C=135°,
∴∠B=180°-30°-135°=15°,
∵FB=FD,
∴∠FDB=∠B=15°,
∴∠DFH=15°+15°=30°,
又∵∠DHF=90°,DF=6![]() ,
,
∴sin∠DFH=![]() ,cos∠DFH=
,cos∠DFH=![]()
∴DH=![]() DF=3
DF=3![]() ,FH=
,FH=![]() DF=9,
DF=9,
∵∠ACD=∠AED=135°,
∴∠DEH=45°,
∴DH=EH=3![]() ,DE=
,DE=![]() DH=
DH=![]() ,
,
∴BH=BF+FH=DF+FH=![]() ,
,
在Rt△DHB中,BD =![]()
∵折叠,
∴CD=DE=![]() ,
,
∴BC=BD+CD=![]()
故答案为:![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2.
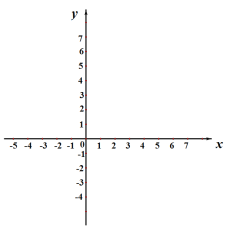
(1)请用含有b的代数式表示c: ;
(2)若点B在直线l上,且B的横坐标为-1,点C的坐标为(b,5).
①若抛物线M还过点B,直接写出该抛物线的解析式;
②若抛物线M与线段BC恰有一个交点,结合函数图象,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() 的图象G经过点
的图象G经过点![]() ,直线
,直线![]() 与y轴交于点B,与图象G交于点C.
与y轴交于点B,与图象G交于点C.
(1)求m的值.
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
①当直线l过点![]() 时,直接写出区域W内的整点个数.
时,直接写出区域W内的整点个数.
②若区域W内的整点不少于4个,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校数学兴趣小组的同学要测量建筑物![]() 的高度,如图,建筑物
的高度,如图,建筑物![]() 前有一段坡度为
前有一段坡度为![]() 的斜坡
的斜坡![]() ,小明同学站在斜坡上的
,小明同学站在斜坡上的![]() 点处,用测角仪测得建筑物屋顶
点处,用测角仪测得建筑物屋顶![]() 的仰角为
的仰角为![]() ,接着小明又向下走了
,接着小明又向下走了![]() 米,刚好到达坡底
米,刚好到达坡底![]() 处,这时测到建筑物屋顶
处,这时测到建筑物屋顶![]() 的仰角为
的仰角为![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面内.若测角仪的高度
在同一平面内.若测角仪的高度![]() 米,则建筑物
米,则建筑物![]() 的高度约为( ).(精确到0.1米,参考数据:
的高度约为( ).(精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() )
)
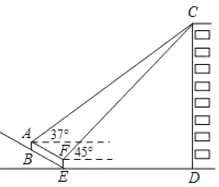
A.38.6B.39.0C.40.0D.41.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数,否则称为合数.
其中,1和0既不是质数也不是合数.
材料二:一个较大自然数是质数还是合数通常用“![]() 法”来判断,主要分为三个步骤:
法”来判断,主要分为三个步骤:
第一步,找出大于![]() 且最接近
且最接近![]() 的平方数
的平方数![]() ;
;
第二步,用小于![]() 的所有质数去除
的所有质数去除![]() ;
;
第三步,如果这些质数都不能整除![]() ,那么
,那么![]() 是质数;如果这些质数中至少有一个能整除
是质数;如果这些质数中至少有一个能整除![]() ,那么
,那么![]() 就是合数.
就是合数.
如何判断239是质数还是合数?
第一步,![]() ;
;
第二步,小于16的质数有:2、3、5、7、11、13,用2、3、5、7、11、13依次去除239;
第三步,发现没有质数能整除239,所以239是质数.
材料三:分解质因数就是把一个合数分解成若干个质数的乘积的形式,通过分解质因数可以确定该合数的约数的个数.若![]() …(
…(![]() ,
,![]() ,
,![]() …是不相等的质数,
…是不相等的质数,![]() ,
,![]() ,
,![]() …是正整数),则合数
…是正整数),则合数![]() 共有
共有![]() …个约数.如
…个约数.如![]() ,
,![]() ,则8共有4个约数;又如
,则8共有4个约数;又如![]() ,
,![]() ,则12共有6个约数.请用以上方法解决下列问题:
,则12共有6个约数.请用以上方法解决下列问题:
(1)请用“![]() 法”判断163是质数还是合数;
法”判断163是质数还是合数;
(2)求有12个约数的最小自然数.
查看答案和解析>>
科目:初中数学 来源: 题型:
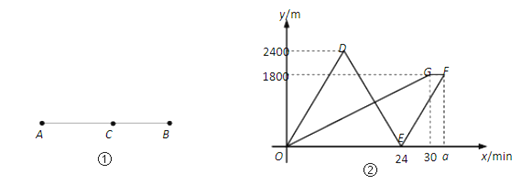
【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.
(1)小明的速度为 m/min,图②中a的值为 .
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.当12≤x≤30时,求出y与x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是由五个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②.则三视图发生改变的是( )

A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图(1)中,在![]() 中,
中,![]() ,垂足为点
,垂足为点![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿射线
的速度沿射线![]() 运动,当点
运动,当点![]() 与点
与点![]() 重合时,运动停止.过点
重合时,运动停止.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 在射线
在射线![]() 上的对应点为点
上的对应点为点![]() ,连接
,连接![]() .若
.若![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,
,![]() 关于
关于![]() 的函数图象如图(2)所示(其中
的函数图象如图(2)所示(其中![]() ,
,![]() ,
,![]() 时,函数解析式不同).
时,函数解析式不同).
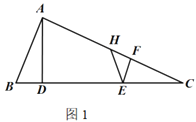
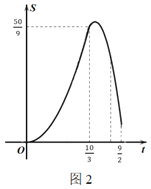
(1)求![]() 的长;
的长;
(2)求![]() 关于
关于![]() 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com