
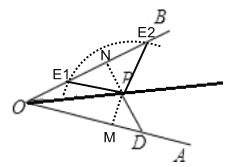
【题目】如图,已知点P为∠AOB的角平分线上的一点,点D在边OA上.在边OB上取一点E,使得PE=PD.
(1)用圆规作出所有符合条件的点E;
(2)写出∠OEP与∠ODP的数量关系,并加以证明.

【答案】(1)见解析;(2)∠OEP=∠ODP或∠OEP+∠ODP=180°.
【解析】
(1)以P为圆心,PD的长为半径画弧交OB于点E1,E2,则E1,E2即为所求;
(2)过点P作PM⊥OD,PN⊥OB,利用HL可证Rt△PNE2≌Rt PMD,得到∠OE2P与∠ODP;由PE1=PE2,可得∠OE2P=∠E2E1P=∠ODP,根据邻补角的性质可得∠OE1P+∠ODP=180°.
解:(1)如图所示,E1,E2即为所求:

(2)∠OEP=∠ODP或∠OEP+∠ODP=180°,
理由是:过点P作PM⊥OD,PN⊥OB,
∵OP是∠AOB的角平分线,
∴PM=PN,
又∵PE2=PD,∠PNE2=∠PMD,
∴Rt△PNE2≌Rt PMD(HL),
∴∠OE2P=∠ODP,
∵PE1=PE2,
∴∠OE2P=∠E2E1P,
∴∠E2E1P=∠ODP,
∵∠OE1P+∠E2E1P=180°,
∴∠OE1P+∠ODP=180°,
∴∠OEP=∠ODP或∠OEP+∠ODP=180°.


科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)x2+8x-20=0(用配方法);
(2)x2-2x-3=0;
(3)(x-1)(x+2)=4(x-1);
(4)3x2-6x=1(用公式法).
查看答案和解析>>
科目:初中数学 来源: 题型:
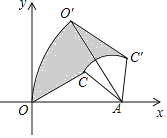
【题目】如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转到△O′AC′,使得点O′的坐标是(1,![]() ),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:
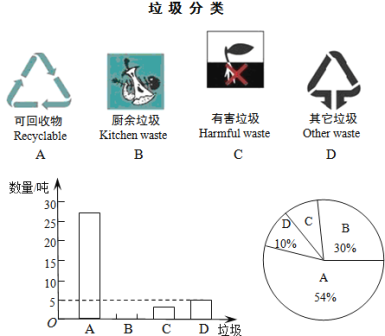
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图样中,产生的有害垃圾C所对应的圆心角 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设该城市每月产生的生活垃圾为1000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过点A(2,0)的直线![]() 与y轴交于点B,与双曲线
与y轴交于点B,与双曲线![]() 交于点P,点P位于y轴左侧,且到y轴的距离为1,已知tan∠OAB=
交于点P,点P位于y轴左侧,且到y轴的距离为1,已知tan∠OAB=![]() .
.
(1)分别求出直线与双曲线相应的函数表达式;
(2)观察图象,直接写出不等式![]() >
>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校“河南省汉子听写大赛初赛”冠军组成员的年龄分布
年龄/岁 | 12 | 13 | 14 | 15 |
人数 | 5 | 15 | x | 12﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A. 平均数、中位数 B. 平均数、方差 C. 众数、中位数 D. 中位数、方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
(1)求![]() 三个顶点
三个顶点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,并用含字母
,并用含字母![]() 的式子表示
的式子表示![]() 的面积(
的面积(![]() );
);
(3)在(2)问的条件下,是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积?如果存在,请求出点
的面积?如果存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
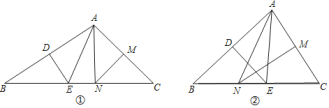
(1)请判断△ANE的周长与AB+AC的和的大小,并说明理由.
(2)①如图①,若∠B=34°,∠C=28°,求![]() 的度数为______;
的度数为______;
②如图②,若![]() ,则
,则![]() 的度数为________;
的度数为________;
③若![]()
![]() ,则
,则![]() 的度数为________.
的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
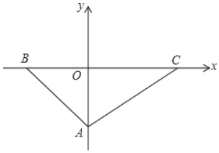
【题目】如图,AB⊥BC且AB=BC,DE⊥CD且DE=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )

A. 36B. 48C. 72D. 108
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com