
70°
【解析】由圆周角∠A=∠C=20°,AB是直径,所以∠ADB=90°,∠ACD=70°.
【解析】(1)①C(2,4),Q(4,0)
②由题意得:P(2t,0),C(2t,-2t+6),Q(6-2t,0)
分两种情况讨论:
情形一:当△AQC∽△AOB时,∠AQC=∠AOB=90°, ∴CQ⊥OA.
∵CP⊥OA,∴点P与点Q重合,OQ=OP,即6-2t=2t,∴t=1.5
情形二:当△ACQ∽△AOB时,∠ACQ=∠AOB=90°,∵OA=OB=6,
∴△AOB是等腰直角三角形,∴△ACQ也是等腰直角三角形,
∵CP⊥OA,∴AQ=2CP,即2t=2(-2t+6),
∴t=2,∴满足条件的t的值是1.5秒或2秒.
(2)①由题意得: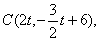
∴以C为顶点的抛物线解析式是 ,
,
由 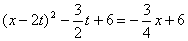 解得
解得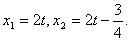
过点D作DE⊥CP于点E,
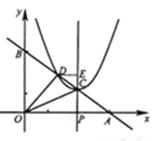
则∠DEC=∠AOB=90°.∵DE∥OA,∴∠EDC=∠OAB,
∴△DEC∽△A OB,∴
OB,∴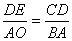 ,∵AO=8,AB=10,
,∵AO=8,AB=10,
DE=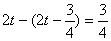 ,∴CD=
,∴CD=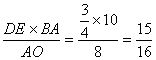
②∵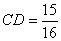 ,CD边上的高=
,CD边上的高= ,
, 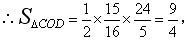
∴S△COD为定值.要使OC边上的高h的值最大,只要OC最短,当OC⊥AB时OC
最短,此时OC的长为 ,∠BCO=90°,∵∠AOB=90°∴∠COP=90°﹣∠BOC=∠OBA,又∵CP⊥OA,∴Rt△PCO∽Rt△OAB.
,∠BCO=90°,∵∠AOB=90°∴∠COP=90°﹣∠BOC=∠OBA,又∵CP⊥OA,∴Rt△PCO∽Rt△OAB.
∴ 即
即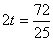 ,∴
,∴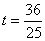
∴当t为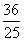 秒时,h的值最大.
秒时,h的值最大.


科目:初中数学 来源: 题型:
如图,在等腰直角三角形ABC和DEC中,∠BCA=∠DCE=90°,点E在边AB上,ED与AC交于点F,连接AD.
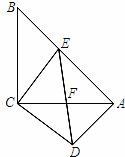
(1)求证:△BCE≌△ACD.
(2)求证:AB⊥AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
C.
【解析】A.如图,反比例函数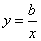 经过第一、三象限,则b>0.所以a<0.则一次函数
经过第一、三象限,则b>0.所以a<0.则一次函数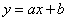 的图象应该经过第一、二、四象限.故本选项错误;
的图象应该经过第一、二、四象限.故本选项错误;
B.如图,反比例函数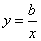 经过第二、四象限,则b<0.所以a>0.则一次函数
经过第二、四象限,则b<0.所以a>0.则一次函数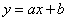 的图象应该经过第一、二、三象限.故本选项错误;
的图象应该经过第一、二、三象限.故本选项错误;
C.如图,反比例函数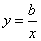 经过第一、三象限,则b>0.所以a<0.则一次函数
经过第一、三象限,则b>0.所以a<0.则一次函数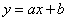 的图象应该经过第一、二、四象限.故本选项正确;
的图象应该经过第一、二、四象限.故本选项正确;
D.如图,反比例函数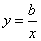 经过第二、四象限,则b<0.所以a>0.则一次函数
经过第二、四象限,则b<0.所以a>0.则一次函数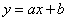 的图象应该经过第一、二、四象限.故本选项错误;
的图象应该经过第一、二、四象限.故本选项错误;
故选C.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两支仪仗队的队员人数相同,平均身高相同,身高的方差分别为S2甲=0.9,S2乙=1.1,则甲、乙两支仪仗队的队员身高更整齐的是 (填“甲”或“乙”).
查看答案和解析>>
科目:初中数学 来源: 题型:
C
【解析】因为AB=AC,∠A=50°,所以∠B=∠C=65°,又因为BD=CE,BE=CF,所以ΔBDE≌ΔCEF,所 以∠BED=∠CFE,因为∠CFE+∠CEF=180°-65°=115°,所以∠BED+∠CEF=115°,所以∠DEF=180°-(∠BED+∠CEF)=180°-115°=65°,
以∠BED=∠CFE,因为∠CFE+∠CEF=180°-65°=115°,所以∠BED+∠CEF=115°,所以∠DEF=180°-(∠BED+∠CEF)=180°-115°=65°,
故选C.
查看答案和解析>>
科目:初中数学 来源: 题型:
铜陵学院毕业生小张响应国家“自主创业”的号召,投资开办了一个装饰品商店,该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系: (1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:
(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系: (1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1)第25天该商店的日销售利润为多少元?
(2)试写出该商店日销售利润y(元)关于销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com