
【题目】已知:平面直角坐标系中,点A在y轴的正半轴上,点B在第二象限, AO= AB,∠BOX=150° .
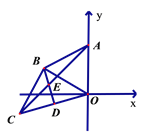
(1)试判定△ABO的形状;
(2)若BC⊥BO,BC=BO,点D为CO的中点,AC、DB交于E,求证:AE=BE+CE.
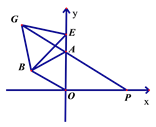
(3)如图:若点E为y轴的正半轴上一动点,以BE为边作等边△BEG,延长GA交x轴于点P,问:AP与AO之间有何数量关系,试证明你的结论.
【答案】(1) △AOB为等边三角形;(2)证明见解析;(3)AP=2AO,理由见解析.
【解析】试题分析:(1)根据∠BOX=150°, ∠AOX=90°,计算出∠AOB=60°,又因为AO= AB,所以可以判定△ABO是等边三角形,(2)在AC上截取AM=CE,先证∠AEB=60°,理由是根据题意可得△AOB为等边三角形, △BOC为等腰直角三角形,确定出∠ABD度数,根据AB=BC,且夹角∠BAC=∠BCA,利用SAS得到△BCM和△BAE全等,利用全等三角形的性质可得BM=BE,得到△BEM是等边三角形,得到BE=EM,由AE=EM+AM,等量代换即可求证,
(3)AP=2AO,理由是根据题意得到BG=BE,AB=OB,
利用等式的性质得到∠ABG=∠OBE=60°,利用外角的性质得到∠APO=30°,在直角三角形中,利用30度所对直角边等于斜边的一半可以得到AP=2AO.
试题解析:(1)∵OB与x轴正半轴夹角为150°,x轴⊥y轴,
∴∠AOB=150°-90°=60°,
∵AO=AB,
∴△AOB为等边三角形,
(2)在AC上截取AM=EC,可得AM+EM=CE+EM,即AE=CM,
∵△AOB为等边三角形, △BOC为等腰直角三角形,
∴∠OBC=90°,∠ABO=60°,
∵D为CO的中点,
∴BD平分∠OBC,即∠CBD=∠OBD=45°,
∴∠ABD=105°,∠ABC=150°,
∴∠BAC=∠BCA=15°,
∴∠AEB=60°,
在△ABE和△CBM中,AB=CB,∠BAE=∠BCM,AE=CM,
∴△ABE≌△CBM(SAS),
∴BM=BE,
∴△BEM为等边三角形,
∴BE=EM,
∴AE=AM+EM=CE+BE,
(3)AP=2AO,理由为:
∵△AOB与△BGE都为等边三角形,
∴BE=BG,AB=OB,∠EBG=∠OBA=60°,
∴∠EBG+∠EBA=∠OBA+∠EBA,即∠ABG=∠OBE,
在△ABG和△OBE中,AB=OB,∠ABG=∠OBE,BE=BG,
∴△ABG≌△OBE(SAS),
∴△ABG≌△OBE(SAS),
∴∠BAG=∠BOE=60°,
∴∠GAO=∠GAB+∠BAO=120°,
∵∠GAO为△AOP的外角,且∠AOP=90°,
∴∠APO=30°,
在Rt△AOP中,∠APO=30°,
则AP=2AO.



科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 一组数据的众数、中位数和平均数不可能是同一个数
B. 一组数据的平均数既不可能大于,也不可能小于这组数据中的所有数据
C. 一组数据的中位数可能与这组数据的任何数据都不相等
D. 众数、中位数和平均数从不同角度描述了一组数据的集中趋势
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量 | 房间价格 | 总维护费用 | |
提价前 | 60 | 200 | 60×20 |
提价后 |
|
|
|
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
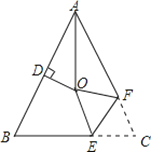
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC= 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答. 
(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
图 | a | b | c | d |
顶点数(S) | 7 | |||
边数(M) | 9 | |||
区域数(N) | 3 |
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有条边.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使(ax2﹣3xy+4y2)﹣(﹣x2+bxy+5y2)=6x2﹣7xy+cy2成立的a,b,c的值依次是( )
A. 7,﹣4,﹣1 B. 5,4,﹣1 C. 7,﹣4,1 D. 5,4,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校积极响应上级的号召,举行了“决不让一个学生因贫困而失学”的捐资助学活动,其中6个班同学的捐款平均数如下表:
班级 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
捐款平均数(元) | 6 | 4.6 | 4.1 | 3.8 | 4.8 | 5.2 |
则这组数据的中位数是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com