
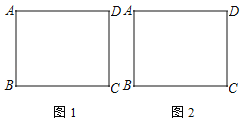
【题目】已知矩形ABCD,其中AD>AB,依题意先画出图形,然后解答问题.
(1)F为DC边上一点,把△ADF沿AF折叠,使点D恰好落在BC上的点E处.在图1中先画出点E,再画出点F,若AB=8,AD=10,直接写出EF的长为 ;
(2)把△ADC沿对角线AC折叠,点D落在点E处,在图2先画出点E,AE交CB于点F,连接BE.求证:△BEF是等腰三角形.
【答案】(1)5;(2)见解析
【解析】
(1)在BC上截取AE=AD得点E,作AF垂直DE交CD于点F(或作∠AED的平分线AF交CD于点F,或作EF垂直AE交CD于点F等等);
(2)作DH垂直AC于点H,延长DH至点E,使HE=DH.方法一证明△ABE≌△CEB(SSS).方法二证明FA=FC即可解决问题.
(1)如图1,以A为圆心,AD长为半径作弧交BC于点E,作AF垂直DE交CD于点F,
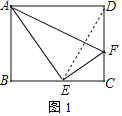
∵四边形ABCD是矩形,
∴AB=CD=8,AD=BC=10,∠B=∠C=90°,
在Rt△ABE中,BE![]() ,
,
∴EC=10﹣6=4,
根据折叠的性质知:EF=DF,
设EF=DF=x,则![]() ,
,
在Rt△EFC中,则有x2=(8﹣x)2+42,
解得 :x=5,
∴EF=5.
故答案为:5;
(2)证明:如图2,作DH垂直AC于点H,延长DH至点E,使HE=DH.

方法1:根据折叠的性质知:△ADC≌△AEC,
∴AD=AE=BC,AB=DC=EC,
在△ABE与△CEB中,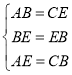 ,
,
∴△ABE≌△CEB(SSS),
∴∠AEB=∠CBE,
∴BF=EF,
∴△BEF是等腰三角形.
方法2:根据折叠的性质知:△ADC≌△AEC,
∴AD=AE=BC,∠DAC=∠EAC,
又∴AD∥BC,
∴∠DAC=∠ACB,
∴∠EAC=∠ACB,
∴FA=FC,
∴FE=FB,
∴△BEF是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.

(1)求证:四边形ADCF是菱形;
(3)若AC=6,AB=8,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,将边BC绕点B逆时针旋转60°,得到线段BE,连接AE,CE.
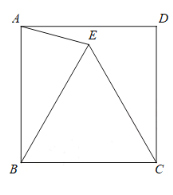
(1)求∠BAE的度数;
(2)连结BD,延长AE交BD于点F.
①求证:DF=EF;
②直接用等式表示线段AB,CF,EF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
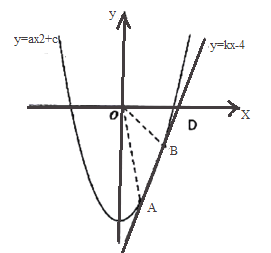
【题目】如图,设抛物线T:y=ax2+c(a> 0)与直线L:y=kx-4(k> 0)交A,B两点(点B在点A的右侧).
(1)如图,若点A(![]() ,-
,-![]() ),且a+c=-1.
),且a+c=-1.
①求抛物线T和直线L的解析式;
②求△AOB的面积.
(2)设点C是点B关于y轴的对称点,当点A,O,C三点共线时,求实数c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线BC与⊙A相切于点C,过B作CB的垂线交⊙O于D,E两点,已知AC=![]() ,CB=a,则以BE,BD的长为两根的一元二次方程是( )
,CB=a,则以BE,BD的长为两根的一元二次方程是( )
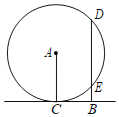
A.x2+bx+a2=0B.x2﹣bx+a2=0C.x2+bx﹣a2=0D.x2﹣bx﹣a2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
由这些数据,科学家推测出植物每天高度增长量![]() 是温度
是温度![]() 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度![]() 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016·荆门中考)如图,天星山山脚下西端A处与东端B处相距800(1+![]() )米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为
)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为![]() 米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
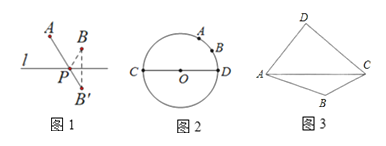
【题目】(理论学习)学习图形变换中的轴对称知识后,我们容易在直线![]() 上找到点
上找到点![]() ,使
,使![]() 的值最小,如图
的值最小,如图![]() 所示,根据这一理论知识解决下列问题:
所示,根据这一理论知识解决下列问题:
(1)(实践运用)如图![]() ,已知
,已知![]() 的直径
的直径![]() 为
为![]() ,弧
,弧![]() 所对圆心角的度数为
所对圆心角的度数为![]() ,点
,点![]() 是弧
是弧![]() 的中点,请你在直径
的中点,请你在直径![]() 上找一点
上找一点![]() ,使
,使![]() 的值最小,并求
的值最小,并求![]() 的最小值.
的最小值.
(2)(拓展延伸)在图![]() 中的四边形
中的四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() .(尺规作图,保留作图痕迹,不必写出作法).
.(尺规作图,保留作图痕迹,不必写出作法).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com