
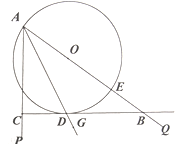
【题目】如图,AG是∠PAQ的平分线,点E在AQ上,以AE为直径的⊙0交AG于点D,过点D作AP的垂线,垂足为点C,交AQ于点B.
(1)求证:直线BC是⊙O的切线;
(2)若⊙O的半径为6,AC=2CD,求BD的长
【答案】(1)证明见详解;(2)8.
【解析】
(1)根据角平分线的定义和同圆的半径相等可得OD∥AC,证明OD⊥CB,可得结论;
(2))在Rt△ACD中,设CD=a,则AC=2a,AD=![]() ,证明△ACD∽△ADE,表示a=
,证明△ACD∽△ADE,表示a=![]() ,由平行线分线段成比例定理得:
,由平行线分线段成比例定理得:![]() ,代入可得结论.
,代入可得结论.
(1)证明:连接OD,
∵AG是∠HAF的平分线,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠CAD=∠ODA,
∴OD∥AC,
∵∠ACD=90°,
∴∠ODB=∠ACD=90°,即OD⊥CB,
∵D在⊙O上,
∴直线BC是⊙O的切线;
(2)解:在Rt△ACD中,设CD=a,则AC=2a,AD=![]() ,
,
连接DE,
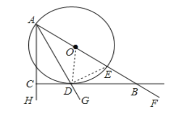
∵AE是⊙O的直径,
∴∠ADE=90°,
由∠CAD=∠BAD,∠ACD=∠ADE=90°,
∴△ACD∽△ADE,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
由(1)知:OD∥AC,
![]()
解得BD=![]()


科目:初中数学 来源: 题型:
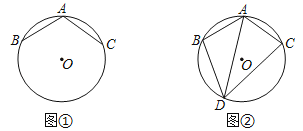
【题目】已知⊙O中,弦AB=AC,∠BAC=120°
(1)如图①,若AB=3,求⊙O的半径.
(2)如图②,点P是∠BAC所对弧上一动点,连接PB、PA、PC,试请判断PA、PB、PC之间的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
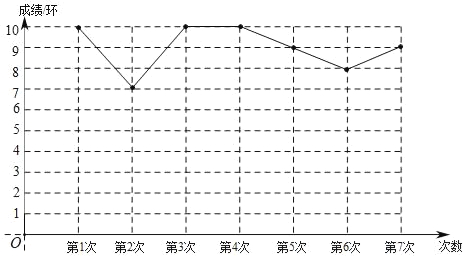
【题目】嘉淇同学利用业余时间进行射击训练,一共射击7次,经过统计,制成如图12所示的折线统计图.
(1)这组成绩的众数是 ;
(2)求这组成绩的方差;
(3)若嘉淇再射击一次(成绩为整数环),得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数,求第8次的射击成绩的最大环数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题发现]
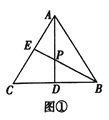
如图①,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,
上,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,则
,则![]() _____ ;
_____ ;
[拓展提高]
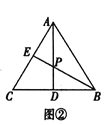
如图②,在等边三角形![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,直线
上,直线![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
[解决问题]
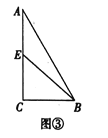
如图③,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,![]() .请直接写出
.请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
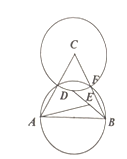
【题目】如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,CF为半径作圆,D是⊙C上一动点,E是BD的中点,当AE最大时,BD的长为( )
A.![]() B.
B.![]() C.4D.6
C.4D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
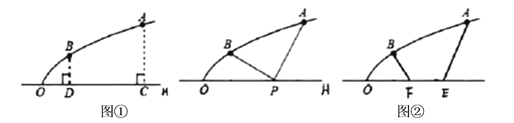
【题目】如图1,是一建筑物造型的纵截面,曲线![]() 是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线
是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线![]() ,
,![]() ,
,![]() 是与水平线
是与水平线![]() 垂直的两根支柱,
垂直的两根支柱,![]() 米,
米,![]() 米,
米,![]() 米.
米.
(1)如图1,为了安全美观,准备拆除支柱![]() 、
、![]() ,在水平线
,在水平线![]() 上另找一点
上另找一点![]() 作为地面上的支撑点,用固定材料连接
作为地面上的支撑点,用固定材料连接![]() 、
、![]() ,对抛物线造型进行支撑加固,用料最省时点
,对抛物线造型进行支撑加固,用料最省时点![]() ,
,![]() 之间的距离是_________.
之间的距离是_________.
(2)如图2,在水平线![]() 上增添一张
上增添一张![]() 米长的椅子
米长的椅子![]() (
(![]() 在
在![]() 右侧),用固定材料连接
右侧),用固定材料连接![]() 、
、![]() ,对抛物线造型进行支撑加固,用料最省时点
,对抛物线造型进行支撑加固,用料最省时点![]() ,
,![]() 之间的距离是_______________.
之间的距离是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
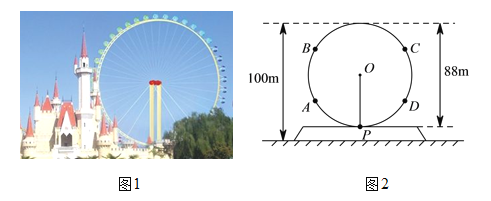
【题目】某游乐园的摩天轮(如图1)有均匀分布在圆形转轮边缘的若干个座舱,人们坐在座舱中可以俯瞰美景,图2是摩天轮的示意图.摩天轮以固定的速度绕中心![]() 顺时针方向转动,转一圈为
顺时针方向转动,转一圈为![]() 分钟.从小刚由登舱点
分钟.从小刚由登舱点![]() 进入摩天轮开始计时,到第12分钟时,他乘坐的座舱到达图2中的点_________处(填
进入摩天轮开始计时,到第12分钟时,他乘坐的座舱到达图2中的点_________处(填![]() ,
,![]() ,
,![]() 或
或![]() ),此点距地面的高度为_______m.
),此点距地面的高度为_______m.
查看答案和解析>>
科目:初中数学 来源: 题型:
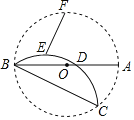
【题目】如图,AB是⊙O的直径,BC是弦,沿BC对折劣弧BC,交AB于D,点E、F分别是弧AB和弧BD的中点.若AD=4,AB=10,则EF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数y=x2+2kx+k﹣1(k为常数),下列说法正确的个数是( )
(1)对任意实数k,函数与x轴有两个交点
(2)当x≥﹣k时,函数y的值都随x的增大而增大
(3)k取不同的值时,二次函数y的顶点始终在同一条抛物线上
(4)对任意实数k,抛物线y=x2+2kx+k﹣1都必定经过唯一定点
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com