
����Ŀ��ijУ���꼶��������ʦΪ�˽Ȿ�꼶ѧ���������˶��İ����������ȡ�˸��꼶����ѧ����������������ƹ����İ�����������˵��飬�������������Ƴ���ͼ��ʾ��������������ͳ��ͼ[˵����ÿλѧ��ֻѡһ���Լ���ϲ����һ�����ࣩ�����������ͼ�ν���������⣺
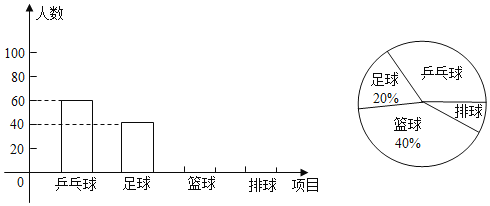
��1���˴α������ѧ��������Ϊ �ˣ�
��2��������ͳ��ͼ���������������ƹ��������������ռ��Բ�ĽǵĶ�����
��3����֪��У��760��ѧ����������ݵ��������ư�������������ѧ�����ж����ˣ�
���𰸡���1��200����2����ȫ����ͳ��ͼ��������ƹ��������������ռ��Բ�ĽǵĶ���Ϊ108������3����������������ѧ������228�ˣ�
��������
��1����ͼ��֪ϲ���������40�ˣ�ռ20%�������������
��2���������������ϲ��ƹ�����������ռ�İٷֱȣ��ó�ϲ��������������ٸ���ϲ�������������ռ�İٷֱ����ϲ��������������Ӷ���ȫͳ��ͼ������ϲ��ƹ�����������ռ�İٷֱȣ����ɵõ�ƹ��������������ռ��Բ�ĽǵĶ�����
��3�����ݰ�������������ѧ����ռ�İٷֱȣ����ɹ��ư�������������ѧ��������
�⣺��1����ϲ���������40�ˣ�ռ20%��
��һ�������ˣ�40��20%=200���ˣ�
�ʴ�Ϊ��200��
��2����ϲ��ƹ��������Ϊ60�ˣ�
����ռ�ٷֱ�Ϊ��![]() ��100%=30%��
��100%=30%��
��ϲ�������������ռ�İٷֱ���1-20%-30%-40%=10%��
��ϲ�����������Ϊ��200��10%=20���ˣ���
��ϲ�����������Ϊ200��40%=80���ˣ���
��������Ϣ��ȫ����ͳ��ͼ�ã�

ƹ��������������ռ��Բ�ĽǵĶ���Ϊ��30%��360��=108����
��3����������������ѧ�����ƣ�760����20%+10%��=228���ˣ���


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��5+����6��+3������9��+����4����7
��2������2��2��8������2����4��|��5|
��3����22��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ȼ��ʳ���A��B���ֲ�Ʒ��ÿ�ݳɱ���Ϊ14Ԫ���ۼ۷ֱ�Ϊ20Ԫ��18Ԫ�������ֲ�Ʒÿ���Ӫҵ�Ϊ1120Ԫ��������Ϊ280Ԫ��
��1���õ�ÿ�����������ֲ�Ʒ�����ٷݣ�
��2���õ�Ϊ����������������A�ֲ�Ʒ���ۼۣ�ͬʱ���B�ֲ�Ʒ���ۼۣ�����ʱ���֣�A�ֲ�Ʒ�ۼ�ÿ��0.5Ԫ�ɶ���1�ݣ�B�ֲ�Ʒ�ۼ�ÿ���0.5Ԫ������1�ݣ���������ֲ�Ʒÿ�������ܷ������䣬��ô�����ֲ�Ʒһ�������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һ�������α��ָ����6����С��ͬ�������Σ�������С�����εı߳���3����ó����γ���___________����ͬһ������������ͼ2�ָ�ָ�����Ͻǵij�����G�����½ǵij�����H�Լ�7�ų�����ͬ��С������M��С������M��ͼ3��ʾ������������G�볤����H���ܳ����ʱ��С������M�Ŀ���________________.
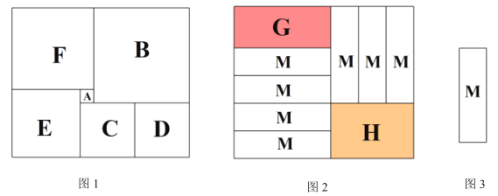
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���֪��AOB=80�㣬OC�ǡ�AOB�ڵ�һ�����ߣ�OD��OE�ֱ�ƽ�֡�BOC�͡�COA��
��1�����DOE�Ķ�����
��2��������OC�Ƶ�O��ת��OB�����ʱ��ͼ��(����ת��OA���Ҳ�ʱ��ͼ��)��OD��OE���ǡ�BOC�͡�COA��ƽ���ߣ���ʱ��DOE�Ĵ�С�Ƿ����1���еĴ���ͬ������ͬ����ѡȡһ�����д����������̣�������ͬ����˵�����ɣ�
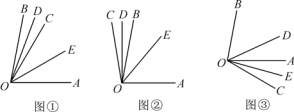
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
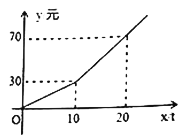
����Ŀ��ij���������磬С���Ӽҳ����ܲ�ȥ�����ڹ�ͣ����һ����ؼң�ͼ�����߱� ʾС���뿪�ҵ�·��y���ף�������ʱ��x���֣�֮��ĺ�����ϵ��������˵���д�����ǣ� ��
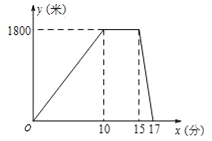
A��С���ڹ���Ϣ��5����
B��С���˳������17��
C��С���ܲ����ٶ�Ϊ180��/��
D�������ƽ���ٶ���900��/��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ���������Լ��ˮ������ˮ��˾���ֶ��շѱ��շѣ���ͼ��ӳ����ÿ��ˮ��![]() ��Ԫ������ˮ��
��Ԫ������ˮ��![]() ���֣�֮��ĺ�����ϵ.
���֣�֮��ĺ�����ϵ.
��1������ˮ������10��ʱ����![]() ����
����![]() �ĺ�������ʽ������д�Ա���ȡֵ��Χ����
�ĺ�������ʽ������д�Ա���ȡֵ��Χ����
��2���������ֶ��շѱ�С�ϼ��������·ݷֱ�ˮ��38Ԫ��27Ԫ�������·ݱ����·ݽ�Լ��ˮ���ٶ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
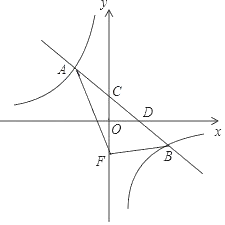
����Ŀ����ƽ��ֱ������ϵ�У�һ�κ���y����![]() x+b��ͼ���뷴��������y��
x+b��ͼ���뷴��������y��![]() ��k��0��ͼ����A��B���㣬��y�ύ�ڵ�C����x�ύ�ڵ�D������A������Ϊ����2��3����
��k��0��ͼ����A��B���㣬��y�ύ�ڵ�C����x�ύ�ڵ�D������A������Ϊ����2��3����
��1����һ�κ����ͷ�������������ʽ��
��2��������C��y������ƽ��4����λ��������F������AF��BF�����ABF�������
��3������ͼ��ֱ��д������ʽ��![]() x+b��
x+b��![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��BD�Ǿ���ABCD�ĶԽ��ߣ�![]() ��
��![]() ����
����![]() ������BD����ƽ�Ƶ�
������BD����ƽ�Ƶ�![]() ��λ�ã�����
��λ�ã�����![]() ��
��![]() ��
��![]() ��
��![]() ����ͼ2��
����ͼ2��
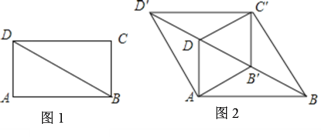
��1����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��2����![]() �˶���ʲôλ��ʱ���ı���
�˶���ʲôλ��ʱ���ı���![]() �����Σ���˵�����ɣ�
�����Σ���˵�����ɣ�
��3���ڣ�2���������£����ı���![]() �����������Խ��������õõ����ĸ�������ƴ�����������ȵľ��Σ�ֱ��д�����п���ƴ�ɵľ����ܳ���
�����������Խ��������õõ����ĸ�������ƴ�����������ȵľ��Σ�ֱ��д�����п���ƴ�ɵľ����ܳ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com