
【题目】如图1,△ABC是边长为8的等边三角形,AD⊥BC于点D,DE⊥AB于点E.

(1)求证:AE=3EB
(2)若点F是AD的中点,点P是BC边上的动点,连接PE,PF,如图2所示,求PE+PF的最小值及此时BP的长;
(3)在(2)的条件下,连接EF,当PE+PF取最小值时,△PEF的面积是______.
【答案】(1)见解析;(2)PE+PF的最小值是6,此时BP的长为2;(3)![]() .
.
【解析】
(1)在三角形BED和三角形ABD中证明![]() 即可;
即可;
(2)作点F关于BC的对称点点G,连接EG交BC于点P,此时PE+PF的值最小等于EG.
作EH⊥AD于H,在直角三角形EGH中求出EG的长即可;可证明△EBP是等边三角形,即可求出BP的长;
(3)证明三角形PEF是直角三角形即可求出面积.
解:(1)如图1,
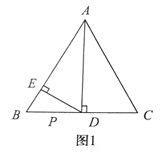
∵△ABC是等边三角形,
∴∠B=![]() ,
,
∵AD⊥BC,DE⊥AB,
∴∠BDE=![]() ,∠BAD=
,∠BAD=![]() ,
,
∴![]()
∴AB=4BE,
∴AE=3BE;
(2)如图2,作点F关于BC的对称点点G,连接EG交BC于点P,此时PE+PF的值最小,
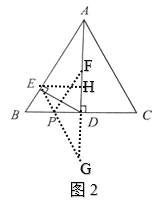
作EH⊥AD于H,
由(1)可知AE=6,∠EAH=![]() ,
,
∴EH=3,AH=![]() ,
,
∵AB=8,∠BAD=![]() ,
,
∴BD=4,AD=![]() ,
,
∴DG=DF=![]() ,DH=
,DH=![]() ,
,
∴GH=![]() ,
,
∴![]() ,
,
∴PE+PF=PE+PG=EG=6,
∴EG=AE,
∴∠G=∠EAH=![]() ,
,
∴∠DPG=![]() ,
,
∴∠EPB=![]() ,
,
∴∠EPB=∠B=![]() ,
,
∴△EBP是等边三角形,
∴BP=BE=2;
∴PE+PF的最小值是6,此时BP的长为2.
(3)如图2,连接EF,
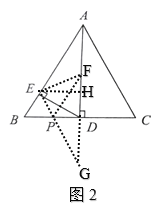
在直角三角形AED中,EF是AD边上的中线,
∴EF=FD=![]() ,
,
∵∠ADE=![]() ,
,
∴△EDF是等边三角形,
∴∠DEF=![]() ,
,
由(2)可知∠BEP=![]() ,
,
∴∠DEP=![]() ,
,
∴∠PEF=![]() ,
,
∴S△PEF=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=BC, BD⊥AC,垂足为D,过点D作DE⊥DF,交AB于点E,交BC于点F.

(1)求证:△DBE≌△DCF;
(2)连接EF,若AE=4,FC=3;求
①EF的长;
②四边形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
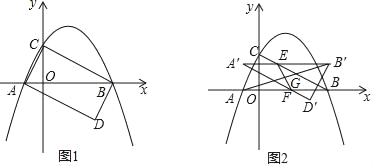
【题目】综合与探究
如图1,抛物线y=ax2+bx+2与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C,连接AC,BC.D为坐标平面第四象限内一点,且使得△ABD与△ABC全等.
(1)求抛物线的表达式.
(2)请直接写出点D的坐标,并判断四边形ACBD的形状.
(3)如图2,将△ABD沿y轴的正方形以每秒1个单位长度的速度平移,得到△A′B′D′,A′B′与BC交于点E,A′D′与AB交于点F.连接EF,AB′,EF与AB′交于点G.设运动的时间为t(0≤t≤2)秒.
①当直线EF经过抛物线的顶点T时,请求出此时t的值;
②请直接写出点G经过的路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
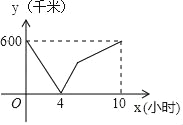
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示:
(1)甲乙两地相距 千米,慢车速度为 千米/小时.
(2)求快车速度是多少?
(3)求从两车相遇到快车到达甲地时y与x之间的函数关系式.
(4)直接写出两车相距300千米时的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在以O为原点的直角坐标系中,抛物线的顶点为A(1,4),且经过点B(2,3),与x轴交于C、D两点.
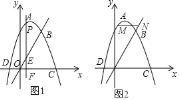
(1)求直线OB的函数表达式和该抛物线的函数表达式;
(2)如图1,点P是x轴上方的抛物线上一动点,过点P作直线PF⊥x轴于点F,交直线OB于点E.若PE=3EF,求出P点的横坐标;
(3)如图2,点M是抛物上的一个动点,且在直线OB的上方,过点M作x轴的平行线与直线OB交于点N,T是抛物线对称轴上一点,当MN最大且△MDT周长最小时,直接写出T的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC是等腰三角形,AB=AC,点D,E,F分别在AB,BC,AC边上,且BD=CE,BE=CF.
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滨海长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,已知行李质量为20kg时需付行李费2元,行李质量为50kg时需付行李费8元.
(1)当行李的质量x超过规定时,求y与x之间的函数表达式.
(2)求旅客最多可免费携带行李的质量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com