
【题目】已知关于x的一元二次方程x2+2x+2k﹣4=0有两个不相等的实数根.
(1)求k的取值范围:
(2)若k为正整数,且该方程的根都是整数,求k的值及该方程的根.
科目:初中数学 来源: 题型:
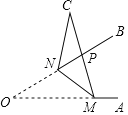
【题目】如图,已知,M,N分别为锐角∠AOB的边OA,OB上的点,ON=6,把△OMN沿MN折叠,点O落在点C处,MC与OB交于点P,若MN=MP=5,则PN=( )
A.2B.3C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
问题情境
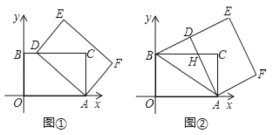
在综合实践课上,老师让同学们探究“平面直角坐标系中的旋转问题”.如图,在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .
.
操作发现
以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() ,
,![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ,
,![]() .
.
(1)如图①,当点![]() 落在
落在![]() 边上时,求点
边上时,求点![]() 的坐标;
的坐标;
继续探究
(2)如图②,当点![]() 落在线段
落在线段![]() 上时,
上时,![]() 与
与![]() 交于点
交于点![]() .
.
①求证![]() ;
;
②求点![]() 的坐标.
的坐标.
拓展探究
(3)如图①,点![]() 是
是![]() 轴上任意一点,点
轴上任意一点,点![]() 是平面内任意一点,是否存在点
是平面内任意一点,是否存在点![]() 使以
使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人轮流在黑板上写下不超过 ![]() 的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
A. 10 B. 9 C. 8D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
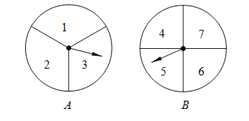
【题目】甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
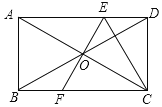
【题目】如图,矩形ABCD,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD、BC于E、F点,连结CE,若OC![]() cm,CD=4cm,则DE的长为( )
cm,CD=4cm,则DE的长为( )
A.![]() cmB.5cmC.3cmD.2cm
cmB.5cmC.3cmD.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
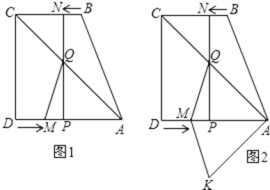
【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.
(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,求 出AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条公路旁依次有![]() ,
,![]() ,
,![]() 三个村庄,甲乙两人骑自行车分别从
三个村庄,甲乙两人骑自行车分别从![]() 村、
村、![]() 村同时出发前往
村同时出发前往![]() 村,甲乙之间的距离
村,甲乙之间的距离![]() 与骑行时间
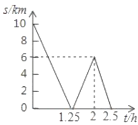
与骑行时间![]() 之间的函数关系如图所示,下列结论:
之间的函数关系如图所示,下列结论:
①![]() ,
,![]() 两村相距
两村相距![]() ; ②出发
; ②出发![]() 后两人相遇;
后两人相遇;
③甲每小时比乙多骑行![]() ; ④相遇后,乙又骑行了
; ④相遇后,乙又骑行了![]() 时两人相距
时两人相距![]() .
.
其中正确的有_____________________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△OAB的三个顶点O(0,0)、A(4,1)、B(4,4)均在格点上.
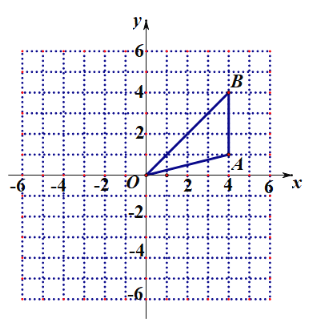
(1)画出△OAB绕原点![]() 顺时针旋转
顺时针旋转![]() 后得到的△
后得到的△![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(2)在(1)的条件下,求线段![]() 在旋转过程中扫过的扇形的面积.
在旋转过程中扫过的扇形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com