

���� ��1�������������ļӷ����ɵô𰸣�
��2������ԲO�ƶ��ľ�����P���ƶ��ľ�����ȣ�P���ƶ����ٶ���ȣ��ɵ÷����飬���ݽⷽ���飬�ɵ�a��b��ֵ�������ٶ���ʱ��Ĺ�ϵ���ɵô𰸣�
��3��������ͬʱ�����ٶȵıȵ���·�̵ıȣ��ɵ�v1��v2��ֵ���������������ε����ʣ��ɵá�ADB=��BDP�����ݵ��������ε��ж����ɵ�BP��DP�Ĺ�ϵ�����ݹ��ɶ������ɵ�DP�ij��������������ļӷ����ɵ�P���ƶ��ľ��룻�������������ε����ʣ��ɵ�EO1�ij����������ۣ�����O�״ε����O1��λ��ʱ������O�ڷ���;�е����O1λ��ʱ������v1��v2��ֵ���ɵô𰸣�
��� �⣺��1����ͼ�٣�Բ��Oȫ�̹��ƶ��� ��2a-8��cm���ú�a�Ĵ���ʽ��ʾ����
�ʴ�Ϊ����2a-8����
��2����Բ��O�ƶ��ľ���Ϊ2��a-4��cm��
�����⣬��
a+2b=2��a-4���٣�
�ߵ�P�ƶ�3�뵽��B������P3s�ƶ���bcm����P�����ƶ�5s����BC���е㣬
����P5���ƶ���$\frac{1}{2}$acm��
��$\frac{b}{3}=\frac{\frac{1}{2}a}{5}$ ��
�ɢ٢ڽ��$\left\{\begin{array}{l}{a=20}\\{b=6}\end{array}\right.$��
�ߵ�P�ƶ����ٶ�Ϊ���O�ƶ��ٶ���ͬ��
���O�ƶ����ٶ�Ϊ$\frac{b}{2}$=$\frac{6}{3}$=2cm��cm/s����
��8��ʱ���ڡ�O�ƶ��ľ���Ϊ8��2=16��cm����
��3���������������
���P�ƶ��ٶ�Ϊv1cm/s����O2�ƶ����ٶ�Ϊv2cm/s��
�����⣬��$\frac{{v}_{1}}{{v}_{2}}$=$\frac{a+2b}{2��a-4��}$=$\frac{20+2��10}{2��20-4��}$=$\frac{5}{4}$��
��ͼ��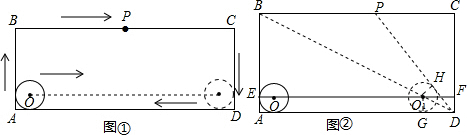
��ֱ��OO1��AB����E�㣬��CD����F�㣬��O1��AD������G�㣬
��PD���O1���У��е�ΪH����O1G=O1H��
�á�DO1G�ա�DO1H��
���ADB=��BDP��
��BC��AD��
���ADB=��CBD
���BDP=��CBD��
��BP=DP��
��BP=xcm����DP=xcm��PC=��20-x��cm��
��Rt��PCD�У��ɹ��ɶ�������
PC2+CD2=PD2������20-x��2+102=x2��
���x=$\frac{25}{2}$
��ʱ��P�ƶ��ľ���Ϊ10+$\frac{25}{2}$=$\frac{45}{2}$��cm����
��EF��AD��
���BEO1�ס�BAD��
��$\frac{E{O}_{1}}{AD}$=$\frac{BE}{BA}$����$\frac{E{O}_{1}}{20}$=$\frac{8}{10}$��
EO1=16cm��OO1=14cm��
�ٵ���O�״ε����O1��λ��ʱ����O�ƶ��ľ���Ϊ14cm��
��ʱ��P���O�ƶ����ٶȱ�Ϊ$\frac{{v}_{1}}{{v}_{2}}$=$\frac{45}{28}$��
��$\frac{45}{28}$��$\frac{5}{4}$��
���ʱPD���O1�������У�
�ڵ���O�ڷ���;�е����O1λ��ʱ����O�ƶ��ľ���Ϊ2��20-4��-14=18cm��
���ʱ��P���O�ƶ����ٶȱ�Ϊ$\frac{{v}_{1}}{{v}_{2}}$=$\frac{45}{36}$=$\frac{5}{4}$��
��ʱPD���O1ǡ�����У�
�ʴ�Ϊ��$\frac{5}{4}$��
���� ���⿼����Բ���ۺ��⣬��1���������������ļӷ�����2��������P���O��·����ȣ��ٶ���ȵó��������ǽ���ؼ���������·����ʱ��Ĺ�ϵ���ó��ٶȣ���������ٶȳ���ʱ��ó��������3�����������ʱ�����ٶȵıȵ���·�̵ıȣ����������ε����ʣ����������ε��ж������ɶ������������ʱ�����ٶȵıȵ���·�̵ı��ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{b}{a}=\frac{b^2}{a^2}$ | B�� | $\frac{b+1}{a+1}=\frac{b}{a}$ | C�� | $\frac{{{a^2}-{b^2}}}{a+b}=a-b$ | D�� | $\frac{a}{-a-b}=-\frac{a}{a-b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y=ax2+2ax+c��a��0����x�ύ��A��-3��0����B���㣨A��B����ࣩ����y�ύ�ڵ�C��0��-3���������ߵĶ���ΪM��
��ͼ��������y=ax2+2ax+c��a��0����x�ύ��A��-3��0����B���㣨A��B����ࣩ����y�ύ�ڵ�C��0��-3���������ߵĶ���ΪM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ��������a���ѳ�����������b��һ��������b�ַ��ѳ�����������c��һ��������c�з��ѳ�����������d�������������ƣ���������f�ĸ�����25��������ݵ���ʽ��ʾ����
��ͼ��һ��������a���ѳ�����������b��һ��������b�ַ��ѳ�����������c��һ��������c�з��ѳ�����������d�������������ƣ���������f�ĸ�����25��������ݵ���ʽ��ʾ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��ADƽ�֡�BAC����BC�ڵ�E��AB=6��AD=5����DE�ij�Ϊ��������
��ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��ADƽ�֡�BAC����BC�ڵ�E��AB=6��AD=5����DE�ij�Ϊ��������| A�� | 2.2 | B�� | 2.5 | C�� | 2 | D�� | 1.8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com