Question

1．如图，在平面直角坐标系中，直线l所在的直线的解析式为y=$\frac{3}{4}$x，点B坐标为（10，0）过B做BC⊥直线l，垂足为C，点P从原点出发沿x轴方向向点B运动，速度为1单位/s，同时点Q从点B出发沿B→C→原点方向运动，速度为2个单位/s，当一个动点到达终点时，另一个动点也随之停止运动．
（1）OC=8，BC=6；
（2）当t=5（s）时，试在直线PQ上确定一点M，使△BCM的周长最小，并求出该最小值；
（3）设点P的运动时间为t（s），△PBQ的面积为y，当△PBQ存在时，求y与t的函数关系式，并写出自变量t的取值范围．

Answer 1

分析 （1）根据勾股定理，可得答案；
（2）根据线段垂直平分线的性质，可得直线PQ上的点到O、C的距离相等，根据两点之间线段最短，可得M点与P点重合，根据三角形的周长，可得答案；
（3）根据速度与时间的关系，可得OP，BQ，根据正弦函数，可得QH，根据三角形的面积公式，可得答案．

解答 解：（1）∵直线l所在的直线的解析式为y=$\frac{3}{4}$x，BC⊥直线l，
∴$\frac{BC}{OC}$=$\frac{3}{4}$．
又∵OB=10，BC=3x，OC=4x，
∴（3x）²+（4x）²=10²，
解得x=2，x=-2（舍），
OC=4x=8，BC=3x=6，
故答案为：8，6；
（2）如图1：，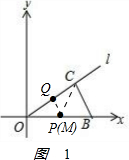
PQ是OC的垂直平分线，OB交PQ于P即M点与P点重合，
M与P点重合时△BCM的周长最小，
周长最小为=BM+PM+BC=OB+BC=10+6=16；
（3）①当0＜t≤3时，过Q作QH⊥OB垂足为H，如图2：，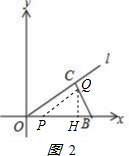
PB=10-t，BQ=2t，HQ=2t•sinB=2t•cos∠COB=2t×$\frac{OC}{OB}$=$\frac{8}{5}$t，
y=$\frac{1}{2}$PB•QH=$\frac{1}{2}$（10-t）$\frac{8}{5}$t=-$\frac{4}{5}$t²+8t；
②当3＜t＜5时，过Q作QH⊥OB垂足为H，如图3：，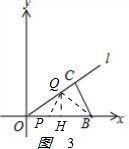
PB=10-t，OQ=OC+BC-2t=14-2t，
QH=OQ•sin∠QOH=（14-2t）$\frac{OC}{OB}$=$\frac{3}{5}$（14-2t）=$\frac{42}{5}$-$\frac{6}{5}$t，
y=$\frac{1}{2}$PB•QH=$\frac{1}{2}$（10-t）（$\frac{42}{5}$-$\frac{6}{5}$t）=$\frac{3}{5}$t²-$\frac{51}{5}$t+42，
综上所述y=$\left\{\begin{array}{l}{-\frac{4}{5}{t}^{2}+8t（0＜t≤3）}\\{\frac{3}{5}{t}^{2}-\frac{51}{5}t+42（3＜t＜5）}\end{array}\right.$．

点评 本题考查了一次函数综合题，利用轴对称的性质得出M与P重合是解题关键；利用锐角三角函数得出QH的长是解题关键，要分类讨论，以防遗漏．