
【题目】如图,现有一个大正方形和四个一样的小正方形,小明、小聪、小方分别用这些正方形设计出了图1,图2,图3三种图案:

(1)根据图1,图2中所标数据,求出大正方形和小正方形的边长分别是多少厘米?
(2)若图3中四个小正方形的重叠部分也是三个一样的小正方形,求大正方形中未被小正方形覆盖的阴影部分的面积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已如点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2019个单位长度没有弹性的细线(线的相细忽略不计)的一端固定在A处,并按![]() 的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.
的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探究平行线的判定——基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行时,老师布置了这样的任务:
请同学们分组在学案上(如图),用直尺和三角尺画出过点P与直线AB平行的直线PQ;并思考直尺和三角尺在画图过程中所起的作用.

小菲和小明所在的小组是这样做的:他们选取直尺和含有45°角的三角尺,用平移三角尺的画图方法画出AB的平行线PQ,并将实际画图过程抽象出平面几何图形(如图).

以下是小菲和小明所在小组关于直尺和三角尺作用的讨论:
①在画平行线的过程中,三角尺由初始位置靠着直尺平移到终止位置,实际上就是先画∠BMD=45°,再过点P画∠BMD=45°
②由初始位置的三角尺和终止位置的三角尺各边所在直线构成一个“三线八角图”,其中QP为截线
③初始位置的三角尺和终止位置的三角尺在“三线八角图”中构成一组同位角
④在画图过程中,直尺可以由直线CD代替
⑤在“三线八角图”中,因为AB和CD是截线,所以,可以下结论“两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行”
其中,正确的是( )
A.①②⑤B.①③④C.②④⑤D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).

(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=![]() (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
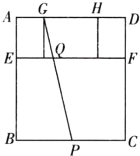
【题目】如图,一个长方形窗框![]() 被
被![]() 分成上下两个长方形,上部分长方形又被分成三个小长方形,其中
分成上下两个长方形,上部分长方形又被分成三个小长方形,其中![]() ,
,![]() 为
为![]() 的四等分点(
的四等分点(![]() 在
在![]() 左侧)且
左侧)且![]() .一晾衣杆斜靠在窗框上的
.一晾衣杆斜靠在窗框上的![]() 位置,
位置,![]() 为
为![]() 中点.若
中点.若![]() ,
,![]() 分长方形
分长方形![]() 的左右面积之比为
的左右面积之比为![]() ,则
,则![]() 分长方形
分长方形![]() 的左右面积之比为________.(用含
的左右面积之比为________.(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川攀枝花12分)如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).

(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D在边BC上,DE⊥AB于E,DH⊥AC于H,且满足DE=DH,F为AE的中点,G为直线AC上一动点,满足DG=DF,若AE=4cm,则AG= _____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )

A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分线 D.∠BAD=120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在真角坐标系中,矩形0ABC的顶点A,C在坐标轴上,点B(4,2);过点D(0,3)和E(6,0)的直线分别与AB、BC交于点M、N.
(1)求直线DE的函数表达式和点M,N的坐标;
(2)若函数y=![]() (k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(3)求△OMN的面积S;
(4)若函教y=![]() (k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.
(k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com