
【题目】(2013年四川攀枝花12分)如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).

(1)求抛物线的解析式;
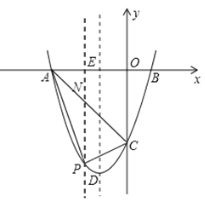
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】解:(1)由于抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),可设抛物线的解析式为:y=a(x+3)(x﹣1),
将C点坐标(0,﹣3)代入,得:a(0+3)(0﹣1)=5,解得 a=1。
∴抛物线的解析式为:y=(x+3)(x﹣1),即y=x2+2x﹣3。
(2)如图1,过点P作x轴的垂线,交AC于点N.
设直线AC的解析式为y=kx+m,由题意,得![]() ,解得
,解得![]() 。
。
∴直线AC的解析式为:y=﹣x﹣3。
设P点坐标为(x,x2+2x﹣3),
则点N的坐标为(x,﹣x﹣3),
∴PN=PE﹣NE=﹣(x2+2x﹣3)+(﹣x﹣3)=﹣x2﹣3x。
∵S△PAC=S△PAN+S△PCN,
∴![]() 。
。
∴当x=![]() 时,S有最大值
时,S有最大值![]() ,此时点P的坐标为(
,此时点P的坐标为(![]() ,
,![]() )。
)。
(3)在y轴上是否存在点M,能够使得△ADE是直角三角形。理由如下:
∵y=x2+2x﹣3=y=(x+1)2﹣4,∴顶点D的坐标为(﹣1,﹣4)。
∵A(﹣3,0),∴AD2=(﹣1+3)2+(﹣4﹣0)2=20。
设点M的坐标为(0,t),分三种情况进行讨论:
①当A为直角顶点时,如图2,
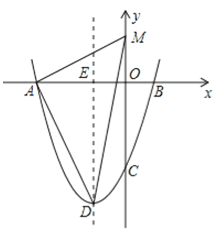
由勾股定理,得AM2+AD2=DM2,
即(0+3)2+(t﹣0)2+20=(0+1)2+(t+4)2,解得t=![]() 。
。
∴点M的坐标为(0,![]() )。
)。
②当D为直角顶点时,如图3,
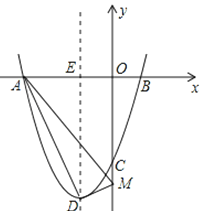
由勾股定理,得DM2+AD2=AM2,
即(0+1)2+(t+4)2+20=(0+3)2+(t﹣0)2,解得t=![]() 。
。
∴点M的坐标为(0,![]() )。
)。
③当M为直角顶点时,如图4,
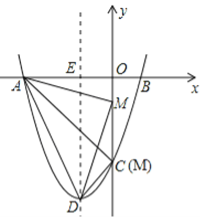
由勾股定理,得AM2+DM2=AD2,
即(0+3)2+(t﹣0)2+(0+1)2+(t+4)2=20,解得t=﹣1或﹣3。
∴点M的坐标为(0,﹣1)或(0,﹣3)。
综上所述,在y轴上存在点M,能够使得△ADE是直角三角形,此时点M的坐标为(0,![]() )或(0,
)或(0,![]() )或(0,﹣1)或(0,﹣3)。
)或(0,﹣1)或(0,﹣3)。
【解析】(1)已知抛物线上的三点坐标,利用待定系数法可求出该二次函数的解析式。
(2)过点P作x轴的垂线,交AC于点N,先运用待定系数法求出直线AC的解析式,设P点坐标为(x,x2+2x﹣3),根据AC的解析式表示出点N的坐标,再根据S△PAC=S△PAN+S△PCN就可以表示出△PAC的面积,运用顶点式就可以求出结论。
(3)分三种情况进行讨论:①以A为直角顶点;②以D为直角顶点;③以M为直角顶点;设点M的坐标为(0,t),根据勾股定理列出方程,求出t的值即可。


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,A,B为格点
(Ⅰ)AB的长等于__
(Ⅱ)请用无刻度的直尺,在如图所示的网格中求作一点C,使得CA=CB且△ABC的面积等于![]() ,并简要说明点C的位置是如何找到的__________________
,并简要说明点C的位置是如何找到的__________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:
①若a>b,则c﹣a<c﹣b;
②若a>0,则![]() =a;
=a;
③对角线互相平分且相等的四边形是菱形;
④如果两条弧相等,那么它们所对的圆心角相等.
其中原命题与逆命题均为真命题的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②AP=BQ;③PQ∥AE;④DE=DP;⑤∠AOE=120°;其中正确结论的个数为( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一个大正方形和四个一样的小正方形,小明、小聪、小方分别用这些正方形设计出了图1,图2,图3三种图案:

(1)根据图1,图2中所标数据,求出大正方形和小正方形的边长分别是多少厘米?
(2)若图3中四个小正方形的重叠部分也是三个一样的小正方形,求大正方形中未被小正方形覆盖的阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,反比例函数y=![]() 的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
(1)求反比例函数与一次函数的解析式及B点坐标;
(2)若C是y轴上的点,且满足△ABC的面积为10,求C点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠ABC=∠ADC,∠BAD=∠BCD B. AB=BC
C. AB=CD,AD=BC D. ∠DAB+∠BCD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,证明:△ABD≌△ACE,DE=BD+CE;
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D, A, E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com