
【题目】4月23日是“世界读书日”,学校开展“让书香溢满校园”读书活动,以提升青少年的阅读兴趣,九年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计,根据所得数据绘制了两幅不完整统计图(每组包括最小值不包括最大值).九年级(1)班每天阅读时间在0.5小时以内的学生占全班人数的8%.根据统计图解答下列问题:
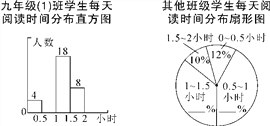
(1)九年级(1)班有 名学生;
(2)补全直方图;
(3)除九年级(1)班外,九年级其他班级每天阅读时间在1~1.5小时的学生有165人,请你补全扇形统计图;
(4)求该年级每天阅读时间不少于1小时的学生有多少人.
【答案】(1)50;(2)见解析;(3)246人.
【解析】试题分析:(1),利用条形统计图与九年级(1)班每天阅读时间在0.5h以内的学生占全班人数的百分比,进而得出该班的人数;
(2),利用班级人数进而得出0.5~1小时的人数,进而得出答案;
(3),利用九年级其他班级每天阅读时间在1~1.5小时的学生有165人,求出1~1.5小时在扇形统计图中所占比例,进而得出0.5~1小时在扇形统计图中所占比例;
(4),利用扇形统计图得出该年级每天阅读时间不少于1小时的人数,进而得出答案.
试题解析:
(1)由题意可得:4÷8%=50(人).
(2)由(1)得:0.5~1小时的为:50-4-18-8=20(人),如图所示.
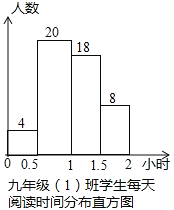
(3)∵除九年(1)班外,九年级其他班级每天阅读时间在1~1.5小时的学生有165人,
∴1~1.5小时在扇形统计图中所占比例=165÷(600-50)×100%=30%.
故0.5~1小时在扇形统计图中所占比例=1-30%-10%-12%=48%.
如图所示:

(4)(600-50)×(30%+10%)+18+8=246(人).
故该年级每天阅读时间不少于1小时的学生有246人.
点睛: 此题主要考查了频数分部直方图以及扇形统计图和条形统计图的应用,利用图形获取正确信息是解题关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
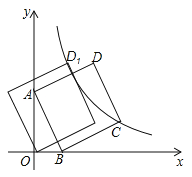
【题目】如图,直线![]() 与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线
与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线![]() (
(![]() )上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线
)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线![]() (
(![]() )上的点D1处,则a= .
)上的点D1处,则a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C,B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.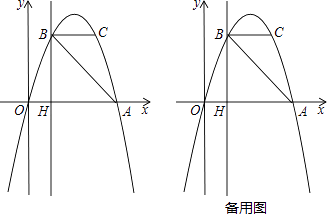
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当CM=MN,且∠CMN=90°时,求此时△CMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为 . 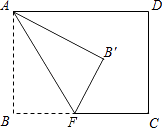
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
阅读材料:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数3与1对应的两点之间的距离为|3﹣1|=2;
在数轴上,有理数5与﹣2对应的两点之间的距离为|5﹣(﹣2)|=7;
在数轴上,有理数﹣2与3对应的两点之间的距离为|﹣2﹣3|=5;
在数轴上,有理数﹣8与﹣5对应的两点之间的距离为|﹣8﹣(﹣5)|=3;……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|a﹣b|或|b﹣a|,记为|AB|=|a﹣b|=|b﹣a|.

解决问题:
(1)数轴上有理数﹣10与﹣5对应的两点之间的距离等于 ;数轴上有理数x与﹣5对应的两点之间的距离用含x的式子表示为 ;若数轴上有理数x与﹣1对应的两点A,B之间的距离|AB|=2,则x等于 ;
联系拓广:
(2)如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为﹣2,动点P表示的数为x.
请从A,B两题中任选一题作答,我选择 题.
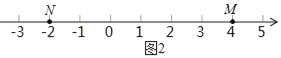
A.①若点P在点M,N两点之间,则|PM|+|PN|= ;
②若|PM|=2|PN|,即点P到点M的距离等于点P到点N的距离的2倍,则x等于 .
B.①若点P在点M,N之间,则|x+2|+|x﹣4|= ;
若|x+2|+|x﹣4|═10,则x= ;
②根据阅读材料及上述各题的解答方法,|x+2|+|x|+|x﹣2|+|x﹣4|的最小值等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(a,0),B(0,b),且a、b满足![]() =0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线
=0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线![]() 经过C、D两点.
经过C、D两点.
(1)求k的值;
(2)点P在双曲线![]() 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,![]() 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠D=135°,AD=6,CE=2![]() ,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )
,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )
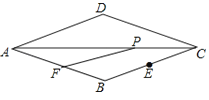
A. 3 B. 6 C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A,B是数轴上的点,请参照图并思考,完成下列各题.

(1) 若点A表示数![]() ,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
(2) 若点A表示数3,将A点向左移动6个单位长度,再向右移动5个单位长度后到达点B,则B表示的数是________;此时 A,B两点间的距离是________.
(3)若A点表示的数为m,将A点向右移动n个单位长度,再向左移动t个单位长度后到达终点B,此时A、B两点间的距离为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com