
����Ŀ����֪ʶ���ɣ�
�����Ѿ�֪����ͨ����ͬ�ķ�����ʾͬһͼ�ε����������̽����Ӧ�ĵ�ʽ��
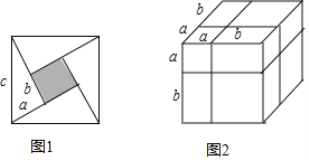
2002��8���ڱ����ٿ��˹�����ѧ��ᣬ�������ͼ1��ʾ���������ĸ���״��С��ȫ��ͬ��ֱ�����������м��С������ƴ�ɵ�һ���������Σ�ֱ�������ε�����ֱ�DZ߳��ֱ�Ϊa��b �� a<b ����б�߳�Ϊc��
��1��ͼ����Ӱ���ֵ���������ַ����ɷֱ��ʾΪ�� �� ���� �� ��
��2�����ܵó���a��b��c֮���������ϵ���� �� ���Ⱥ������軯Ϊ�����ʽ����
��3��һֱ�������ε�����ֱ�DZ߳�Ϊ6��8������б�߳�Ϊ�� �� ��
��֪ʶǨ�ƣ�
ͨ����ͬ�ķ�����ʾͬһ������������Ҳ����̽����Ӧ�ĵ�ʽ����ͼ2�DZ߳�Ϊa+b�������壬����ͼ��ʾ�ķָ��߷ֳ�8�飮
��4���ò�ͬ�����������������������Ϳ��Եõ�һ����ʽ�������ʽ����Ϊ�� �� �����Ⱥ������軯Ϊ�����ʽ��
��5����֪a+b��3��ab��1����������Ĺ�����a3+b3��ֵ��
���𰸡���1��c2��2ab����b��a��2����2��a2+b2��c2����3��10����4����a+b��3��a3+b3+3a2b+3ab2����5��a3+b3��18��
��������
��1�����ͼ�εĸ������ֵ���������ɵó��𰸣�
��2�����ݣ�1���Ľ�������ɵó��𰸣�
��3������������ɣ�
��4�������������������������ֵ���������ɵó��𰸣�
��5�����루4���еĵ�ʽ������ɣ�
�⣺
��1������c2��2ab����b��a��2��
��2������a2+b2��c2��
��3������10��
��4��ͼ�ε����Ϊ��a+b��3��a3+b3+a2b+a2b+a2b+ab2+ab2+ab2��
����a+b��3��a3+b3+3a2b+3ab2��
�ʴ�Ϊ����a+b��3��a3+b3+3a2b+3ab2��
��5����a+b��3��ab��1����a+b��3��a3+b3+3a2b+3ab2����a3+b3+3ab��a+b��
��33��a3+b3+3��1��3��
��ã�a3+b3��18��


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д� ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
�У�![]() ����A��B�ֱ�����������.
����A��B�ֱ�����������.
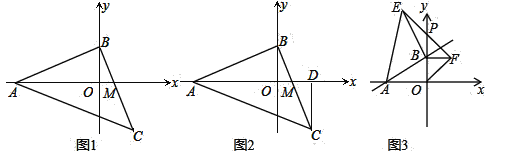
��1����ͼ1����![]() ��
��![]() ����C������ꣻ
����C������ꣻ
��2����ͼ2��CD��ֱx����D�㣬�ж�CD��OA��OD��������ϵ����֤����Ľ��ۣ�
��3����ͼ3������A������Ϊ![]() ����B��y������������˶�ʱ���ֱ���OB��ABΪ���ڵ�һ���ڶ�����������
����B��y������������˶�ʱ���ֱ���OB��ABΪ���ڵ�һ���ڶ�����������![]() ������
������![]() ������EF��y����P�㣬����B��y�����ƶ�ʱ��PB�ij����Ƿ�仯������������PBֵ������仯��PB��ȡֵ��Χ.
������EF��y����P�㣬����B��y�����ƶ�ʱ��PB�ij����Ƿ�仯������������PBֵ������仯��PB��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
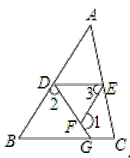
����Ŀ����������������̣�
��֪����ͼ����1+��2��180�㣬��3����B
��֤����EDG+��DGC��180��
֤�����ߡ�1+��2��180������֪��
��1+��DFE��180�㣨�� ����
���2���� ������ ����
��EF��AB���� ����
���3���� ������ ����
�֡ߡ�3����B����֪��
���B����ADE���� ����
��DE��BC���� ����
���EDG+��DGC��180�㣨�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����л���ͳ�Ļ�������ij��ѧ��������ѧ������Ȥ�����齨������ȤС�飬���ѧУ�����ȡ�˲���ͬѧ����Ȥ���ý��е��飬���ռ����������������Ƴ���������ͳ��ͼ�������ͼ�е���Ϣ������������⣺
��1��ѧУ��ε��鹲��ȡ���� ����ѧ����
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У���Ϸ�����������ε�Բ�ĽǶ���Ϊ�� ����
��4�����У����ѧ��2000����������Ƹ�У�ж�����ѧ��ϲ���鷨��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
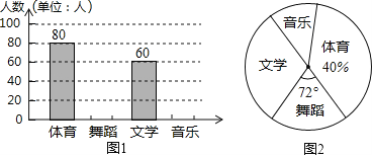
����Ŀ��Ϊ�˴ٽ�ѧ����������չ��ij��ѧÿ������֯ѧ����չ���Ż���ֱ��������������赸����ѧ���������ţ�Ҫ�����˲μ����ţ�����ÿ��ֻ�ܲμ�һ���Ϊ�˽�ѧ��ϲ���������Ż��ѧУ��֯ѧ�����Ա�����ȡ����ѧ�������ʾ����飬�����ռ��������ݣ����Ƴ���������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺
��1���˴ι�������______��ѧ����
��2��������ͳ��ͼ����������
��3��ͼ2�����������������ε�Բ�ĽǵĶ���Ϊ______��
��4������У����ѧ��1600�ˣ����Ƹ�Уϲ���������ŵ�ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����C��ֱ��AB�ϣ�AC=8cm��BC=6cm����M��N�ֱ���AC��BC���е㣬���߶�MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ʵ�Ա�ﳵ���ʾֳ��������������� 2 km ���� A �壬������������ 3 km ���� B �壬 Ȼ�������� 9 km ���� C �壬���ص��ʾ�.
(1)���ʾ�Ϊԭ�㣬������Ϊ�������� 1 cm ��ʾ 1 km �����ᣬ���ڸ������ϱ�ʾ A��B��C ������ׯ��λ�ã�
(2)C ���� A ���ж�Զ��
(3)�ʵ�Աһ�������˶���ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��OΪ����ԭ�㣬�ı���OABCΪ���Σ�A��10��0����C��0��4������D��OA���е㣬��P��BC���˶�������ODP������Ϊ5�ĵ���������ʱ����P�������Ϊ�� ��

A. ��3��4����2��4�� B. ��2��4����8��4��
C. ��3��4����8��4�� D. ��3��4����2��4����8��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ˮ�ۡ���ַ����г����۸�������ˮ��Դ���á�ˮ������ڵȷ�������ã���չ��ˮ���ϵ��Ŀռ䣬��ǿ����ҵ�;���Ľ�ˮ��ʶ��������ˮ��Դ���˷ѣ�����ʽ����ˮ�۽�ˮ�۷�Ϊ���λ��߶�Σ�ÿһ�ֶζ���һ�����ֲ���ĵ�λˮ�ۣ����ǵ�λˮ�ۻ����ź�ˮ���ֶζ����ӣ�ij�ء�����ˮ�ۡ��շѱ����±������¼��㣩��
��ˮ�� (��λ��m3 ) | ���ۣ�Ԫ/m3 �� |
������ | 2 |
���� | 3 |
���� | 5 |
���磺�õ���ij������3�·���ˮ![]() m3����Ӧ��ˮ��Ϊ
m3����Ӧ��ˮ��Ϊ![]() ��Ԫ
��Ԫ![]() ��
��
�����ϱ������ݽ���������⣺
��1���û���5�·���ˮ16 m3������û�5�·�Ӧ��ˮ�Ѷ���Ԫ��
��2���û���5�·ݽ�ˮ��50Ԫ������û�5�·ݵ���ˮ��Ϊ����m3��
��3�� �û���5��6�����¹���ˮ![]() m3������6�·���ˮ��������
m3������6�·���ˮ��������![]() m3����5�·���ˮ
m3����5�·���ˮ![]() m3�����ú�
m3�����ú�![]() ��ʽ�ӱ�ʾ�û�����5��6�����¹�����ˮ�ѣ�
��ʽ�ӱ�ʾ�û�����5��6�����¹�����ˮ�ѣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com