
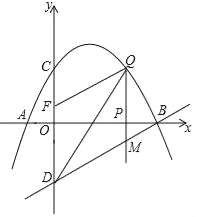
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)点P在线段AB上运动的过程中,是否存在点Q,使得△BOD∽△QBM?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)已知点F(0,![]() ),点P在x轴上运动,试求当m为何值时以D、M、Q、F为顶点的四边形是平行四边形.
),点P在x轴上运动,试求当m为何值时以D、M、Q、F为顶点的四边形是平行四边形.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)存在,点Q的坐标为(3,2);(3)m=﹣1或m=3或m=1+
x+2;(2)存在,点Q的坐标为(3,2);(3)m=﹣1或m=3或m=1+![]() 或1﹣
或1﹣![]() 时,四边形DMQF是平行四边形.
时,四边形DMQF是平行四边形.
【解析】
(1)根据待定系数法求解可得;
(2)利用△BOD∽△QBM得![]() ,再证△MBQ∽△BPQ得
,再证△MBQ∽△BPQ得![]() ,解之即可得此时m的值.
,解之即可得此时m的值.
(3)先利用待定系数法求出直线BD解析式为y=![]() x-2,则Q(m,-
x-2,则Q(m,-![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m-2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得.
m-2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得.
(1)由抛物线过点A(﹣1,0)、B(4,0)可设解析式为y=a(x+1)(x﹣4),
将点C(0,2)代入,得:﹣4a=2,
解得:a=﹣![]() ,
,
则抛物线解析式为y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)如图所示:
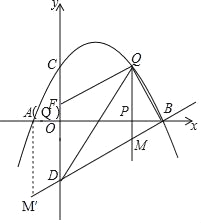
∵当△BOD∽△QBM时,
则![]() ,
,
∵∠MBQ=90°,
∴∠MBP+∠PBQ=90°,
∵∠MPB=∠BPQ=90°,
∴∠MBP+∠BMP=90°,
∴∠BMP=∠PBQ,
∴△MBQ∽△BPQ,
∴![]() ,
,
∴![]() ,
,
解得:m1=3、m2=4,
当m=4时,点P、Q、M均与点B重合,不能构成三角形,舍去,
∴m=3,点Q的坐标为(3,2);
(3)由题意知点D坐标为(0,﹣2),
设直线BD解析式为y=kx+b,
将B(4,0)、D(0,﹣2)代入,得:![]() ,
,
解得: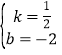 ,
,
∴直线BD解析式为y=![]() x﹣2,
x﹣2,
∵QM⊥x轴,P(m,0),
∴Q(m,﹣![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m﹣2),
m﹣2),
则QM=﹣![]() m2+
m2+![]() m+2﹣(
m+2﹣(![]() m﹣2)=﹣
m﹣2)=﹣![]() m2+m+4,
m2+m+4,
∵F(0,![]() )、D(0,﹣2),
)、D(0,﹣2),
∴DF=![]() ,
,
∵QM∥DF,
∴当|﹣![]() m2+m+4|=
m2+m+4|=![]() 时,四边形DMQF是平行四边形,
时,四边形DMQF是平行四边形,
解得:m=﹣1或m=3或m=1+![]() 或1﹣
或1﹣![]()
即m=﹣1或m=3或m=1+![]() 或1﹣
或1﹣![]() 时,四边形DMQF是平行四边形.
时,四边形DMQF是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.

(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论:
①△BDF,△CEF都是等腰三角形;
②DE=BD+CE;
③△ADE的周长为AB+AC;
④BD=CE.其中正确的是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图
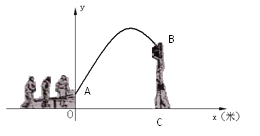
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形。
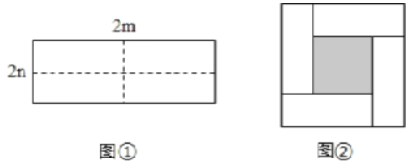
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:![]() ;
;
方法二:![]() .
.
(2)(m+n)![]() ,(mn)
,(mn) ![]() ,mn这三个代数式之间的等量关系为___
,mn这三个代数式之间的等量关系为___
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求xy的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
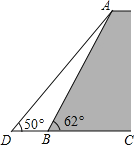
【题目】如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com