Question

14．如图，抛物线y=$\frac{1}{2}$x²+mx+n与直线y=-$\frac{1}{2}$x+3交于A，B两点，交x轴与D，C两点，连接AC，BC，已知A（0，3），C（3，0）．
（1）求抛物线的解析式；
（2）求tan∠BAC的值；
（3）设E为线段AC上一点（不含端点），连接DE，一动点M从点D出发，沿线段DE以每秒一个单位速度运动到E点，再沿线段EA以每秒$\sqrt{2}$个单位的速度运动到A后停止，当点E的坐标是多少时，点M在整个运动中用时最少？

Answer 1

分析 （1）根据待定系数法，可得函数解析式；
（2）根据解方程组，可得B点坐标，根据直角三角形的性质，可得BC，AC，根据角的和差，可得∠ACB的度数，根据正切函数的定义，可得答案；
（3）根据锐角三角函数，可得AE与NE的关系，根据路程与速度，可得DE+EN，根据两点之间线段最短，可得DE+EN=D′E+EN，根据矩形的判定与性质，可得ND′=OC=3，ON=D′C=DC，根据线段的和差，可得ON，
根据直角三角形的性质，可得NE的长，可得答案．

解答 解：（Ⅰ）把A（0，3），C（3，0）代入y=$\frac{1}{2}$x²+mx+n，得
$\left\{\begin{array}{l}{\frac{1}{2}×9+3m+n=0}\\{n=3}\end{array}\right.$．
解得$\left\{\begin{array}{l}{m=-\frac{5}{2}}\\{n=3}\end{array}\right.$．
∴抛物线的解析式为y=$\frac{1}{2}$x²-$\frac{5}{2}$x+3．
（2）联立$\left\{\begin{array}{l}{y=-\frac{1}{2}x+3}\\{y=\frac{1}{2}{x}^{2}-\frac{5}{2}x+3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$（不符合题意，舍），$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$，
∴点B的坐标为（4，1）．
过点B作BH⊥x轴于H，如图1．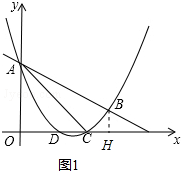
∵C（3，0），B（4，1），
∴BH=1，OC=3，OH=4，CH=4-3=1，
∴BH=CH=1．
∵∠BHC=90°，
∴∠BCH=45°，BC=$\sqrt{2}$．
同理：∠ACO=45°，AC=3$\sqrt{2}$，
∴∠ACB=180°-45°-45°=90°，
∴tan∠BAC=$\frac{BC}{AC}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$；
（3）过点E作EN⊥y轴于N，如图2．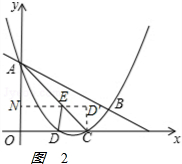
在Rt△ANE中，EN=AE•sin45°=$\frac{\sqrt{2}}{2}$AE，即AE=$\sqrt{2}$EN，
∴点M在整个运动中所用的时间为$\frac{DE}{1}$+$\frac{EA}{\sqrt{2}}$=DE+EN．
作点D关于AC的对称点D′，连接D′E，
则有D′E=DE，D′C=DC，∠D′CA=∠DCA=45°，
∴∠D′CD=90°，DE+EN=D′E+EN．
根据两点之间线段最短可得：
当D′、E、N三点共线时，DE+EN=D′E+EN最小．
此时，∵∠D′CD=∠D′NO=∠NOC=90°，
∴四边形OCD′N是矩形，
∴ND′=OC=3，ON=D′C=DC．
对于y=$\frac{1}{2}$x²-$\frac{5}{2}$x+3，当y=0时，有$\frac{1}{2}$x²-$\frac{5}{2}$x+3=0，
解得：x₁=2，x₂=3．
∴D（2，0），OD=2，
∴ON=DC=OC-OD=3-2=1，
∴NE=AN=AO-ON=3-1=2，
∴点E的坐标为（2，1）．

点评 本题考查了二次函数综合题，利用待定系数法求函数解析式；利用直角三角的性质得出BC，AC的长是解题关键，又利用了正切函数的定义；利用两点之间线段最短得出EN+DE=ND′是解题关键，又利用了矩形的判定与性质．