
【题目】如图,已知![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]()
(1)请在网格中,画出线段![]() 关于原点对称的线段
关于原点对称的线段![]() ;
;
(2)请在网格中,过点![]() 画一条直线
画一条直线![]() ,将
,将![]() 分成面积相等的两部分,与线段
分成面积相等的两部分,与线段![]() 相交于点
相交于点![]() ,写出点
,写出点![]() 的坐标;
的坐标;
(3)若另有一点![]() ,连接
,连接![]() ,则
,则![]() .
.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元;购买
元;购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元.
元.
(1)求购买一个甲种文具、一个乙种文具各需多少元?
(2)若学校计划购买这两种文具共![]() 个,投入资金不少于
个,投入资金不少于![]() 元又不多于
元又不多于![]() 元,设购买甲种文具
元,设购买甲种文具![]() 个,求有多少种购买方案?
个,求有多少种购买方案?
(3)设学校投入资金![]() 元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】齐齐哈尔市教育局想知道某校学生对扎龙自然保护区的了解程度,在该校随机抽取了部分学生进行问卷,问卷有以下四个选项:A.十分了解;B.了解较多:C.了解较少:D.不了解(要求:每名被调查的学生必选且只能选择一项).现将调查的结果绘制成两幅不完整的统计图.请根据两幅统计图中的信息回答下列问题:
(1)本次被抽取的学生共有_______名;
(2)请补全条形图;
(3)扇形图中的选项“C.了解较少”部分所占扇形的圆心角的大小为_______°;
(4)若该校共有![]() 名学生,请你根据上述调查结果估计该校对于扎龙自然保护区“十分了解”和“了解较多”的学生共有多少名?
名学生,请你根据上述调查结果估计该校对于扎龙自然保护区“十分了解”和“了解较多”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】岳阳市整治农村“空心房”新模式,获评全国改革开放40年地方改革创新40案例.据了解,我市某地区对辖区内“空心房”进行整治,腾退土地1200亩用于复耕和改造,其中复耕土地面积比改造土地面积多600亩.
(1)求复耕土地和改造土地面积各为多少亩?
(2)该地区对需改造的土地进行合理规划,因地制宜建设若干花卉园和休闲小广场,要求休闲小广场总面积不超过花卉园总面积的![]() ,求休闲小广场总面积最多为多少亩?
,求休闲小广场总面积最多为多少亩?
查看答案和解析>>
科目:初中数学 来源: 题型:
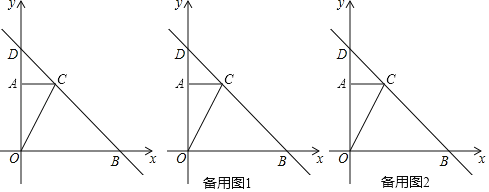
【题目】如图,在平面直角坐标系中,Rt△AOC的直角边OA在y轴正半轴上,且顶点O与坐标原点重合,点C的坐标为(1,2),直线y=﹣x+b过点C,与x轴交于点B,与y轴交于点D.
(1)B点的坐标为 ,D点的坐标为 ;
(2)动点P从点O出发,以每秒1个单位长度的速度,沿O→A→C的路线向点C运动,同时动点Q从点B出发,以相同速度沿BO的方向向点O运动,过点Q作QH⊥x轴,交线段BC或线段CO于点H.当点P到达点C时,点P和点Q都停止运动,在运动过程中,设动点P运动的时间为t秒:
①设△CPH的面积为S,求S关于t的函数关系式;
②是否存在以Q、P、H为顶点的三角形的面积与S相等?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,AD是
,AD是![]() 的角平分线,且
的角平分线,且![]() ,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
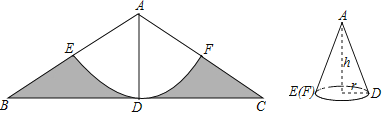
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
查看答案和解析>>
科目:初中数学 来源: 题型:
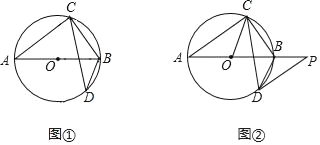
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BCD=28°.
(I)如图①,求∠ABD的大小;
(Ⅱ)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
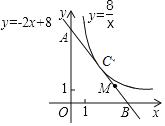
【题目】如图,已知一次函数y=﹣2x+8的图象与坐标轴交于A,B两点,并与反比例函数![]() 的图象相切于点C.
的图象相切于点C.
(1)切点C的坐标是 ;
(2)若点M为线段BC的中点,将一次函数y=﹣2x+8的图象向左平移m(m>0)个单位后,点C和点M平移后的对应点同时落在另一个反比例函数![]() 的图象上时,求k的值.
的图象上时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赤峰市某中学为庆祝“世界读书日”,响应”书香校园”的号召,开展了“阅读伴我成长”的读书活动.为了解学生在此次活动中的读书情况,从全校学生中随机抽取一部分学生进行调查,将收集到的数据整理并绘制成如图所示不完整的折线统计图和扇形统计图.
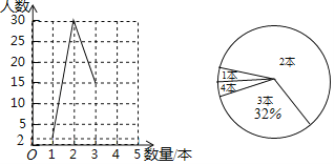
(1)随机抽取学生共 名,2本所在扇形的圆心角度数是 度,并补全折线统计图;
(2)根据调查情况,学校决定在读书数量为1本和4本的学生中任选两名学生进行交流,请用树状图或列表法求这两名学生读书数量均为4本的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com