
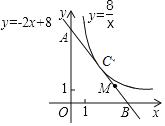
【题目】如图,已知一次函数y=﹣2x+8的图象与坐标轴交于A,B两点,并与反比例函数![]() 的图象相切于点C.
的图象相切于点C.
(1)切点C的坐标是 ;
(2)若点M为线段BC的中点,将一次函数y=﹣2x+8的图象向左平移m(m>0)个单位后,点C和点M平移后的对应点同时落在另一个反比例函数![]() 的图象上时,求k的值.
的图象上时,求k的值.
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是BC边上一点,且AD=BD,⊙O是△ACD的外接圆
(1)求证:直线AB是⊙O的切线;
(2)若AB=10,BC=16,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]()
(1)请在网格中,画出线段![]() 关于原点对称的线段
关于原点对称的线段![]() ;
;
(2)请在网格中,过点![]() 画一条直线
画一条直线![]() ,将
,将![]() 分成面积相等的两部分,与线段
分成面积相等的两部分,与线段![]() 相交于点
相交于点![]() ,写出点
,写出点![]() 的坐标;
的坐标;
(3)若另有一点![]() ,连接
,连接![]() ,则
,则![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
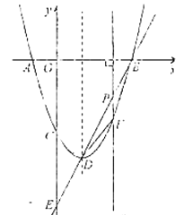
(Ⅰ)求顶点![]() 的坐标;
的坐标;
(Ⅱ)如图,设点![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点![]() .求
.求![]() 的面积最大值;
的面积最大值;
(Ⅲ)点![]() 在线段
在线段![]() 上,当
上,当![]() 时,求点
时,求点![]() 的坐标(直接写出结果,不必写解答过程).
的坐标(直接写出结果,不必写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
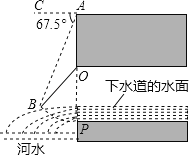
【题目】如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中OP为下水管道口直径,OB为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径OB=OP=100cm,OA为检修时阀门开启的位置,且OA=OB.
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达OB位置时,在点A处测得俯角∠CAB=67.5°,若此时点B恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
(![]() =1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
=1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
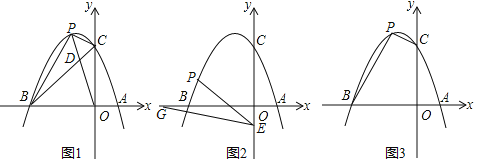
【题目】已知抛物线y=ax2+bx+3经过点A(1,0)和点B(﹣3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)抛物线的解析式为 ,抛物线的顶点坐标为 ;
(2)如图1,连接OP交BC于点D,当S△CPD:S△BPD=1:2时,请求出点D的坐标;
(3)如图2,点E的坐标为(0,﹣1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标;
(4)如图3,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com