
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
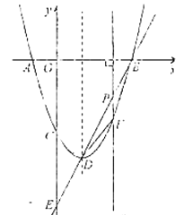
(Ⅰ)求顶点![]() 的坐标;
的坐标;
(Ⅱ)如图,设点![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点![]() .求
.求![]() 的面积最大值;
的面积最大值;
(Ⅲ)点![]() 在线段
在线段![]() 上,当
上,当![]() 时,求点
时,求点![]() 的坐标(直接写出结果,不必写解答过程).
的坐标(直接写出结果,不必写解答过程).
【答案】(Ⅰ)(1,-4);(Ⅱ)1;(Ⅲ)(![]() ,-
,-![]() )
)
【解析】
(Ⅰ)利用待定系数法把![]() ,
,![]() ,代入二次函数
,代入二次函数![]() 中,即可算出b、c的值,得到函数解析式,再用配方法求得顶点
中,即可算出b、c的值,得到函数解析式,再用配方法求得顶点![]() 的坐标;
的坐标;
(Ⅱ)先根据B、D两点坐标利用待定系数法确定直线BD的解析式,设点P的坐标为(m,n),再根据![]() ,得出
,得出![]() 关于点P的横坐标m的函数关系式,利用配方法即可得出结论;
关于点P的横坐标m的函数关系式,利用配方法即可得出结论;
(Ⅲ)根据B、C、D三点的坐标,利用两点间的距离公式分别求出CD、BD、CB的平方,再利用勾股定理的逆定理确定![]() BCD为直角三角形,求出tan∠CDB的值,设点Q的坐标为(n,2n-6),再根据已知条件得出tan∠QCE=3,从而列出n的方程,解方程即可确定Q点坐标.
BCD为直角三角形,求出tan∠CDB的值,设点Q的坐标为(n,2n-6),再根据已知条件得出tan∠QCE=3,从而列出n的方程,解方程即可确定Q点坐标.
(Ⅰ)∵抛物线y=x2-bx+c的图象经过点A(-1,0),B(3,0),
∴![]() ;
;
解得:![]()
∴抛物线的解析式为y=x2-2x-3=(x-1)2-4;
∴顶点![]() 的坐标为:(1,-4);
的坐标为:(1,-4);
(Ⅱ)设直线BD解析式为y=kx+b,
∵![]() ,D(1,-4).
,D(1,-4).
∴![]() ;
;
解得:![]()
∴直线BD解析式为y=2x-6,
设点P的坐标为(m,n),
∵点![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),
∴点P的坐标为:(m,2m-6)(1![]() );
);
∵点![]() 是过点
是过点![]() 作
作![]() 轴的垂线与抛物线的交点.
轴的垂线与抛物线的交点.
∴点F的坐标为:(m,m2-2m-3);
∵点P在点F的上方,
∴PF=(2m-6)-(m2-2m-3)=-m2+4m-3
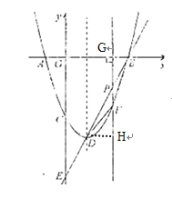
设直线PF交x轴于点G,过点D作DH⊥PF于H,
∵![]()
=-m2+4m-3=-![]() .
.
∴![]() 是关于m的二次函数;
是关于m的二次函数;
∵a=-1![]() ,
,
∴当m=2时,![]() 的面积有最大值,最大值为1.
的面积有最大值,最大值为1.
(Ⅲ)点Q的坐标为(![]() ,-
,-![]() )
)
连接BC、CD,由点![]() 、
、![]() 、
、![]() (1,-4);
(1,-4);
根据两点间的距离公式可得:![]() ,
,![]() ,
,
![]() ;
;
∴![]()
∴∠DCB=90°
在Rt![]() 中,tan∠CDB=
中,tan∠CDB=![]()
∵∠CDB=∠QCE,∴tan∠QCE =3,
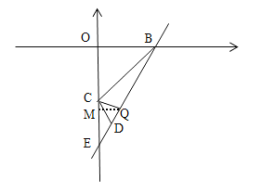
设点Q的坐标为(n,2n-6)
过点Q作QM⊥CE于M,
在Rt![]() 中,tan∠QCE=
中,tan∠QCE=![]() =3,∴n=
=3,∴n=![]()
∴点Q的坐标为(![]() ,-
,-![]() )
)


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】已知:在正方形ABCD中,AB=3,E是边BC上一个动点(点E不与点B,点C重合),连接AE,点H是BC延长线上一点.过点B作BF⊥AE,交AE于点G,交DC于点F.
(1)求证:AE=BF;
(2)过点E作EM⊥AE,交∠DCH的平分线于点M,连接FM,判断四边形BFME的形状,并说明理由;
(3)在(2)的条件下,∠EMC的正弦值为![]() ,求四边形AGFD的面积.
,求四边形AGFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】岳阳市整治农村“空心房”新模式,获评全国改革开放40年地方改革创新40案例.据了解,我市某地区对辖区内“空心房”进行整治,腾退土地1200亩用于复耕和改造,其中复耕土地面积比改造土地面积多600亩.
(1)求复耕土地和改造土地面积各为多少亩?
(2)该地区对需改造的土地进行合理规划,因地制宜建设若干花卉园和休闲小广场,要求休闲小广场总面积不超过花卉园总面积的![]() ,求休闲小广场总面积最多为多少亩?
,求休闲小广场总面积最多为多少亩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,AD是
,AD是![]() 的角平分线,且
的角平分线,且![]() ,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
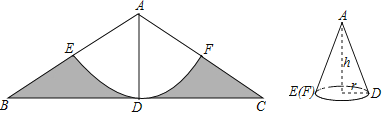
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
查看答案和解析>>
科目:初中数学 来源: 题型:
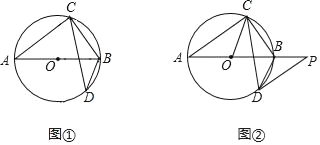
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BCD=28°.
(I)如图①,求∠ABD的大小;
(Ⅱ)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
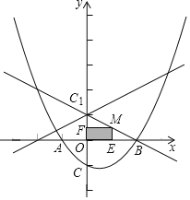
【题目】如图,已知抛物线y=ax2+bx﹣1与x轴的交点为A(﹣1,0),B(2,0),且与y轴交于C点.
(1)求该抛物线的表达式;
(2)点C关于x轴的对称点为C1,M是线段BC1上的一个动点(不与B、C1重合),ME⊥x轴,MF⊥y轴,垂足分别为E、F,当点M在什么位置时,矩形MFOE的面积最大?说明理由.
(3)已知点P是直线y=![]() x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.
x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
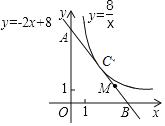
【题目】如图,已知一次函数y=﹣2x+8的图象与坐标轴交于A,B两点,并与反比例函数![]() 的图象相切于点C.
的图象相切于点C.
(1)切点C的坐标是 ;
(2)若点M为线段BC的中点,将一次函数y=﹣2x+8的图象向左平移m(m>0)个单位后,点C和点M平移后的对应点同时落在另一个反比例函数![]() 的图象上时,求k的值.
的图象上时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组 ,请结合题意填空,完成本题的解答.
,请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_________;
(Ⅱ)解不等式②,得_________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 边上从点
边上从点![]() 运动到点
运动到点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,连
,连![]() ,在点
,在点![]() 运动过程中,请探究以下问题:
运动过程中,请探究以下问题:
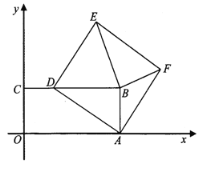
(1)![]() 的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
(2)若![]() 为等腰三角形,求此时正方形
为等腰三角形,求此时正方形![]() 的边长.
的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com