
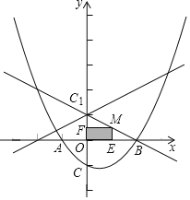
【题目】如图,已知抛物线y=ax2+bx﹣1与x轴的交点为A(﹣1,0),B(2,0),且与y轴交于C点.
(1)求该抛物线的表达式;
(2)点C关于x轴的对称点为C1,M是线段BC1上的一个动点(不与B、C1重合),ME⊥x轴,MF⊥y轴,垂足分别为E、F,当点M在什么位置时,矩形MFOE的面积最大?说明理由.
(3)已知点P是直线y=![]() x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.
x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.
【答案】(1) ![]() ;(2)点M为线段C1B中点时,S矩形MFOE最大,理由见解析;(3) 点P和点Q的坐标为P1(4,3),Q1(4,5)或P2(﹣2,0),Q2(﹣2,2)或P3(2,2),Q3(2,0)或P4(﹣2,0),Q4(2,0).
;(2)点M为线段C1B中点时,S矩形MFOE最大,理由见解析;(3) 点P和点Q的坐标为P1(4,3),Q1(4,5)或P2(﹣2,0),Q2(﹣2,2)或P3(2,2),Q3(2,0)或P4(﹣2,0),Q4(2,0).
【解析】
(1)将A(﹣1,0),B(2,0)分别代入解析式即可解答
(2)令x=0,y=﹣1,得出C的坐标,再利用对称轴的性质得出C1,将B(2,0),C1(0,1)分别代入直线C1B解析式,得出直线C1B的解析式,设M(t,![]() ),则 E(t,0),F(0,
),则 E(t,0),F(0,![]() ),根据矩形的面积公式即可解答
),根据矩形的面积公式即可解答
(3)根据题意可分情况讨论①当C1C为边,则C1C∥PQ,C1C=PQ,设P(m,![]() m+1),Q(m,
m+1),Q(m,![]() ),求出m即可解答;②C1C为对角线,∵C1C与PQ互相平分,C1C的中点为(0,0),PQ的中点为(0,0),设P(m,
),求出m即可解答;②C1C为对角线,∵C1C与PQ互相平分,C1C的中点为(0,0),PQ的中点为(0,0),设P(m,![]() m+1),则Q(﹣m,
m+1),则Q(﹣m,![]() ),求出m即可
),求出m即可
(1)将A(﹣1,0),B(2,0)分别代入抛物线y=ax2+bx﹣1中,得![]() ,解得:
,解得:
∴该抛物线的表达式为:![]() .
.
(2)在![]() 中,令x=0,y=﹣1,∴C(0,﹣1)
中,令x=0,y=﹣1,∴C(0,﹣1)
∵点C关于x轴的对称点为C1,
∴C1(0,1),设直线C1B解析式为y=kx+b,将B(2,0),C1(0,1)分别代入得![]() ,解得
,解得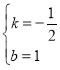 ,
,
∴直线C1B解析式为![]() ,设M(t,
,设M(t,![]() ),则 E(t,0),F(0,
),则 E(t,0),F(0,![]() )
)
∴S矩形MFOE=OE×OF=t(![]() )=﹣
)=﹣![]() (t﹣1)2+
(t﹣1)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当t=1时,S矩形MFOE最大值=![]() ,此时,M(1,
,此时,M(1,![]() );即点M为线段C1B中点时,S矩形MFOE最大.
);即点M为线段C1B中点时,S矩形MFOE最大.
(3)由题意,C(0,﹣1),C1(0,1),以C、C1、P、Q为顶点的四边形为平行四边形,分以下两种情况:
①C1C为边,则C1C∥PQ,C1C=PQ,设P(m,![]() m+1),Q(m,
m+1),Q(m,![]() ),
),
∴|(![]() )﹣(
)﹣(![]() m+1)|=2,解得:m1=4,m2=﹣2,m3=2,m4=0(舍),
m+1)|=2,解得:m1=4,m2=﹣2,m3=2,m4=0(舍),
P1(4,3),Q1(4,5);P2(﹣2,0),Q2(﹣2,2);P3(2,2),Q3(2,0)
②C1C为对角线,∵C1C与PQ互相平分,C1C的中点为(0,0),
∴PQ的中点为(0,0),设P(m,![]() m+1),则Q(﹣m,
m+1),则Q(﹣m,![]() )
)
∴(![]() m+1)+(
m+1)+(![]() )=0,解得:m1=0(舍去),m2=﹣2,
)=0,解得:m1=0(舍去),m2=﹣2,
∴P4(﹣2,0),Q4(2,0);
综上所述,点P和点Q的坐标为:P1(4,3),Q1(4,5)或P2(﹣2,0),Q2(﹣2,2)或P3(2,2),Q3(2,0)或P4(﹣2,0),Q4(2,0).


科目:初中数学 来源: 题型:
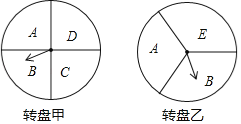
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为 ;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的图象的一部分与
)的图象的一部分与![]() 轴的交点
轴的交点![]() 在
在![]() 与
与![]() 之间,对称轴为直线
之间,对称轴为直线![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤当
为实数);⑤当![]() 时,
时,![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
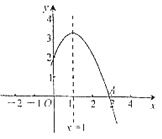
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
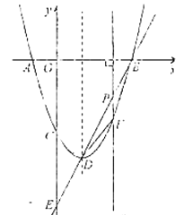
(Ⅰ)求顶点![]() 的坐标;
的坐标;
(Ⅱ)如图,设点![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点![]() .求
.求![]() 的面积最大值;
的面积最大值;
(Ⅲ)点![]() 在线段
在线段![]() 上,当
上,当![]() 时,求点
时,求点![]() 的坐标(直接写出结果,不必写解答过程).
的坐标(直接写出结果,不必写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等
(1)若从中只录用一人,恰好选到思政专业毕业生的概率是 :
(2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3经过点A(1,0)和点B(﹣3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)抛物线的解析式为 ,抛物线的顶点坐标为 ;
(2)如图1,连接OP交BC于点D,当S△CPD:S△BPD=1:2时,请求出点D的坐标;
(3)如图2,点E的坐标为(0,﹣1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标;
(4)如图3,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.
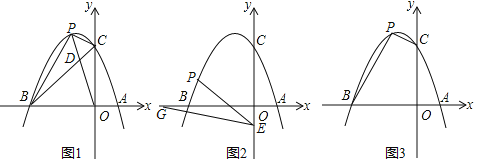
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是大小相等的边长为1的正方形构成的网格,![]() ,
,![]() ,
,![]() ,
,![]() 均为格点.
均为格点.![]() 与
与![]() 交于点
交于点![]() .
.
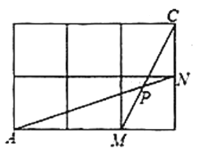
[1].![]() 的值为_________.
的值为_________.
[2].现只有无刻度的直尺,请在给定的网格中作出一个格点三角形.要求:①三角形中含有与![]() 大小相等的角;②可借助该三角形求得
大小相等的角;②可借助该三角形求得![]() 的三角函数值.请并在横线上简单说明你的作图方法.____________.
的三角函数值.请并在横线上简单说明你的作图方法.____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ),
),![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求该抛物线的解析式,并写出它的对称轴;
(2)点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知![]() ,若
,若![]() 是抛物线上一个动点(其中
是抛物线上一个动点(其中![]() ),连接
),连接![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
(4)若点![]() 为抛物线对称轴上一点,抛物线上是否存在点
为抛物线对称轴上一点,抛物线上是否存在点![]() ,使得以
,使得以![]() 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点
为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com