
°æƒø°ø»ÁÕº£¨‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨“—÷™≈◊ŒÔœş![]() ”Î
”Î![]() ÷·Ωª”Ğ
÷·Ωª”Ğ![]() £©£¨
£©£¨![]() ¡Ωµ„£¨”Î
¡Ωµ„£¨”Î![]() ÷·Ωª”е„
÷·Ωª”е„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £Æ
£Æ
£®1£©«Û∏√≈◊ŒÔœşµƒΩ‚Œˆ Ω£¨≤¢–¥≥ˆÀ¸µƒ∂‘≥∆÷·£ª
£®2£©µ„![]() Œ™≈◊ŒÔœş∂‘≥∆÷·…œ“ªµ„£¨¡¨Ω”
Œ™≈◊ŒÔœş∂‘≥∆÷·…œ“ªµ„£¨¡¨Ω”![]() £¨»Ù
£¨»Ù![]() £¨«Ûµ„
£¨«Ûµ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
£®3£©“—÷™![]() £¨»Ù
£¨»Ù![]() «≈◊ŒÔœş…œ“ª∏ˆ∂ص„£®∆‰÷–
«≈◊ŒÔœş…œ“ª∏ˆ∂ص„£®∆‰÷–![]() £©£¨¡¨Ω”
£©£¨¡¨Ω”![]() £¨«Û
£¨«Û![]() √ʪ˝µƒ◊Ó¥Û÷µº∞¥À ±µ„
√ʪ˝µƒ◊Ó¥Û÷µº∞¥À ±µ„![]() µƒ◊¯±Í£Æ
µƒ◊¯±Í£Æ
£®4£©»Ùµ„![]() Œ™≈◊ŒÔœş∂‘≥∆÷·…œ“ªµ„£¨≈◊ŒÔœş…œ «∑ҥʑе„
Œ™≈◊ŒÔœş∂‘≥∆÷·…œ“ªµ„£¨≈◊ŒÔœş…œ «∑ҥʑе„![]() £¨ πµ√“‘
£¨ πµ√“‘![]() Œ™∂•µ„µƒÀƒ±ş–Œ «∆Ω––Àƒ±ş–Œ£ø»Ù¥Ê‘Ğ£¨«Î÷±Ω”–¥≥ˆÀ˘”–¬˙◊„ú˛µƒµ„
Œ™∂•µ„µƒÀƒ±ş–Œ «∆Ω––Àƒ±ş–Œ£ø»Ù¥Ê‘Ğ£¨«Î÷±Ω”–¥≥ˆÀ˘”–¬˙◊„ú˛µƒµ„![]() µƒ◊¯±Í£ª»Ù≤ª¥Ê‘Ğ£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ◊¯±Í£ª»Ù≤ª¥Ê‘Ğ£¨«ÎÀµ√˜¿Ì”…£Æ

°æ¥∞∏°ø£®1£©![]() £¨∂‘≥∆÷·
£¨∂‘≥∆÷·![]() £ª£®2£©
£ª£®2£©![]() £ª£®3£©√ʪ˝”–◊Ó¥Û÷µ «
£ª£®3£©√ʪ˝”–◊Ó¥Û÷µ «![]() £¨
£¨![]() £ª£®4£©¥Ê‘е„
£ª£®4£©¥Ê‘е„![]() πµ√“‘
πµ√“‘![]() Œ™∂•µ„µƒÀƒ±ş–Œ «∆Ω––Àƒ±ş–Œ£¨
Œ™∂•µ„µƒÀƒ±ş–Œ «∆Ω––Àƒ±ş–Œ£¨![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() .
.
°æΩ‚Œˆ°ø
£®1£©Ω´µ„A£®-1£¨0£©£¨B£®3£¨0£©¥˙»Îy=ax2+bx+2º¥ø…£ª
£®2£©π˝µ„D◊˜DG°Õy÷·”ĞG£¨◊˜DH°Õx÷·”ĞH£¨…˵„D£®1£¨y£©£¨‘ĞRt°˜CGD÷–£¨CD2=CG2+GD2=£®2-y£©2+1£¨‘ĞRt°˜BHD÷–£¨BD2=BH2+HD2=4+y2£¨ø…“‘÷§√˜CD=BD£¨º¥ø…«Ûyµƒ÷µ£ª
£®3£©π˝µ„E◊˜EQ°Õy÷·”е„Q£¨π˝µ„F◊˜÷±œşFR°Õy÷·”ĞR£¨π˝µ„E◊˜FP°ÕFR”ĞP£¨÷§√˜Àƒ±ş–ŒQRPE «æÿ–Œ£¨∏˘æıS°˜CEF=Sæÿ–ŒQRPE-S°˜CRF-S°˜EFP£¨¥˙»Î±şº¥ø…£ª
£®4£©∏˘æı∆Ω––Àƒ±ş–Œ∂‘±ş∆Ω––«“œ‡µ»µƒ–‘÷ ø…“‘µ√µΩ¥Ê‘е„M πµ√“‘B£¨C£¨M£¨NŒ™∂•µ„µƒÀƒ±ş–Œ «∆Ω––Àƒ±ş–Œ£¨µ„M£®2£¨2£©ªÚM£®4£¨- ![]() £©ªÚM£®-2£¨-
£©ªÚM£®-2£¨-![]() £©£ª
£©£ª
Ω‚£∫£®1£©Ω´µ„![]() ¥˙»Î
¥˙»Î![]() £¨
£¨
ø…µ√![]() £¨
£¨
![]() £ª
£ª
![]() ∂‘≥∆÷·
∂‘≥∆÷·![]() £ª
£ª
£®2£©»ÁÕº1£∫π˝µ„![]() ◊˜
◊˜![]() ÷·”Ğ
÷·”Ğ![]() £¨◊˜
£¨◊˜![]() ÷·”Ğ
÷·”Ğ![]() £¨
£¨

…˵„![]() £¨
£¨
![]() £¨
£¨
![]() ‘Ğ
‘Ğ![]() ÷–£¨
÷–£¨![]() £¨
£¨
![]() ‘Ğ
‘Ğ![]() ÷–£¨
÷–£¨![]() £¨
£¨
‘Ğ![]() ÷–£¨
÷–£¨![]()
![]() £¨
£¨
![]()
![]()
![]() £¨
£¨
![]() £ª
£ª
£®3£©»ÁÕº2£∫π˝µ„![]() ◊˜
◊˜![]() ÷·”е„
÷·”е„![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜÷±œş
◊˜÷±œş![]() ÷·”Ğ
÷·”Ğ![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() ”Ğ
”Ğ![]() £¨
£¨

![]() £¨
£¨
![]() Àƒ±ş–Œ
Àƒ±ş–Œ![]() «æÿ–Œ£¨
«æÿ–Œ£¨
![]() £¨
£¨
![]() £¨
£¨
![]()
![]()
![]() £¨
£¨
![]()
![]() µ±
µ±![]() ±£¨√ʪ˝”–◊Ó¥Û÷µ «
±£¨√ʪ˝”–◊Ó¥Û÷µ «![]() £¨
£¨
¥À ±![]() £ª
£ª
£®4£©¥Ê‘е„![]() πµ√“‘
πµ√“‘![]() Œ™∂•µ„µƒÀƒ±ş–Œ «∆Ω––Àƒ±ş–Œ£¨
Œ™∂•µ„µƒÀƒ±ş–Œ «∆Ω––Àƒ±ş–Œ£¨
…Ë![]() £¨
£¨
¢ŸÀƒ±ş–Œ![]() «∆Ω––Àƒ±ş–Œ ±£¨
«∆Ω––Àƒ±ş–Œ ±£¨
![]()
![]()
![]()
¢ĞÀƒ±ş–Œ![]() ±∆Ω––Àƒ±ş–Œ ±£¨
±∆Ω––Àƒ±ş–Œ ±£¨
![]()
![]() £¨
£¨
![]() £ª
£ª
¢ğÀƒ±ş–Œ![]() ±∆Ω––Àƒ±ş–Œ ±£¨
±∆Ω––Àƒ±ş–Œ ±£¨
![]() £¨
£¨
![]() £¨
£¨
![]() £ª
£ª
◊ğ…œÀ˘ ˆ£∫![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() £ª
£ª


 ª•∂ØøŒÃ√œµ¡–¥∞∏
ª•∂ØøŒÃ√œµ¡–¥∞∏ º§ªÓÀºŒ¨÷«ƒİ—µ¡∑øŒ ±µº—ß¡∑œµ¡–¥∞∏
º§ªÓÀºŒ¨÷«ƒİ—µ¡∑øŒ ±µº—ß¡∑œµ¡–¥∞∏
| ƒÍº∂ | ∏ş÷–øŒ≥à | ƒÍº∂ | ≥÷–øŒ≥à |
| ∏ş“ª | ∏ş“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥“ª | ≥“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş∂˛ | ∏ş∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥∂˛ | ≥∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş»˝ | ∏ş»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥»˝ | ≥»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
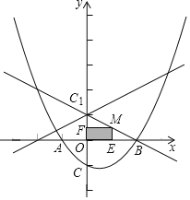
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœşy£Ωax2+bx©Å1”Îx÷·µƒΩªµ„Œ™A(©Å1£¨0)£¨B(2£¨0)£¨«“”Îy÷·Ωª”ĞCµ„.
(1)«Û∏√≈◊ŒÔœşµƒ±Ì¥Ô Ω£ª
(2)µ„Cπÿ”Ğx÷·µƒ∂‘≥∆µ„Œ™C1£¨M «œş∂ŒBC1…œµƒ“ª∏ˆ∂ص„(≤ª”ÎB°¢C1÷ÿ∫œ)£¨ME°Õx÷·£¨MF°Õy÷·£¨¥π◊„∑÷±Œ™E°¢F£¨µ±µ„M‘Ğ ≤√¥Œª÷√ ±£¨æÿ–ŒMFOEµƒ√ʪ˝◊Ó¥Û£øÀµ√˜¿Ì”….
(3)“—÷™µ„P «÷±œşy£Ω![]() x+1…œµƒ∂ص„£¨µ„QŒ™≈◊ŒÔœş…œµƒ∂ص„£¨µ±“‘C°¢C1°¢P°¢QŒ™∂•µ„µƒÀƒ±ş–ŒŒ™∆Ω––Àƒ±ş–Œ ±£¨«Û≥ˆœ‡”¶µƒµ„P∫Õµ„Qµƒ◊¯±Í.
x+1…œµƒ∂ص„£¨µ„QŒ™≈◊ŒÔœş…œµƒ∂ص„£¨µ±“‘C°¢C1°¢P°¢QŒ™∂•µ„µƒÀƒ±ş–ŒŒ™∆Ω––Àƒ±ş–Œ ±£¨«Û≥ˆœ‡”¶µƒµ„P∫Õµ„Qµƒ◊¯±Í.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™°˜ABCƒĞΩ””Ğ°—O£¨¡¨Ω”OA£¨OB£¨OC£¨…Ë°œOAC£Ω¶¡£¨°œOBA£Ω¶¬£¨°œOCB£Ω¶√£Æ‘Úœ¬¡–– ˆ÷–’˝»∑µƒ”–£®°°°°£©
¢Ÿ»Ù¶¡£º¶¬£¨¶¡£º¶√£¨«“OC°ŒAB£¨‘Ú¶√£Ω90°„©Å¶¡£ª
¢Ğ»Ù¶¡£∫¶¬£∫¶√£Ω1£∫4£∫3£¨‘Ú°œACB£Ω30°„£ª
¢ğ»Ù¶¬£º¶¡£¨¶¬£º¶√£¨‘Ú¶¡+¶√©Å¶¬£Ω90°„£ª
¢İ»Ù¶¬£º¶¡£¨¶¬£º¶√£¨‘Ú°œBAC+°œABC£Ω¶¡+¶√©Å2¶¬£Æ
A. ¢Ÿ¢ĞB. ¢ğ¢İC. ¢Ÿ¢Ğ¢ğD. ¢Ÿ¢Ğ¢ğ¢İ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨°˜ABC «µ»—¸÷±Ω«»˝Ω«–Œ£¨°œBAC£Ω 90°„£¨AB£ΩAC£¨Àƒ±ş–ŒADEF «’˝∑Ω–Œ£¨µ„B°¢C∑÷±‘бşAD°¢AF…œ£¨¥À ±BD£ΩCF£¨BD°ÕCF≥…¡¢£Æ

£®1£©µ±°˜ABC»∆µ„AƒÊ ±’Ζ˝◊™¶»£®0°„£º¶»£º90°„£© ±£¨»ÁÕº2£¨BD£ΩCF≥…¡¢¬£ø»Ù≥…¡¢£¨«Î÷§√˜£ª»Ù≤ª≥…¡¢£¨«ÎÀµ√˜¿Ì”…£Æ
£®2£©µ±°˜ABC»∆µ„AƒÊ ±’Ζ˝◊™45°„ ±£¨»ÁÕº3£¨—”≥§DBΩªCF”е„H.
¢Ÿ«Û÷§£∫BD°ÕCF£ª
¢Ğµ±AB£Ω2£¨AD£Ω3![]() ±£¨«Ûœş∂ŒDHµƒ≥§£Æ
±£¨«Ûœş∂ŒDHµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨æÿ–Œ
÷–£¨æÿ–Œ![]() µƒ∂•µ„
µƒ∂•µ„![]() ◊¯±ÍŒ™
◊¯±ÍŒ™![]() £¨µ„
£¨µ„![]() ‘Ğ
‘Ğ![]() ±ş…œ¥”µ„
±ş…œ¥”µ„![]() ‘À∂ØµΩµ„
‘À∂ØµΩµ„![]() £¨“‘
£¨“‘![]() Œ™±ş◊˜’˝∑Ω–Œ
Œ™±ş◊˜’˝∑Ω–Œ![]() £¨¡¨
£¨¡¨![]() £¨‘е„
£¨‘е„![]() ‘À∂Øπ˝≥Ã÷–£¨«ÎÃΩæø“‘œ¬Œ £∫
‘À∂Øπ˝≥Ã÷–£¨«ÎÃΩæø“‘œ¬Œ £∫
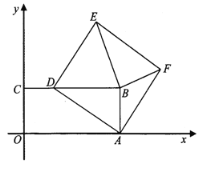
£®1£©![]() µƒ√ʪ˝ «∑Ò∏ƒ±‰£¨»Áπ˚≤ª±‰£¨«Û≥ˆ∏√∂®÷µ;»Áπ˚∏ƒ±‰£¨«ÎÀµ√˜¿Ì”…;
µƒ√ʪ˝ «∑Ò∏ƒ±‰£¨»Áπ˚≤ª±‰£¨«Û≥ˆ∏√∂®÷µ;»Áπ˚∏ƒ±‰£¨«ÎÀµ√˜¿Ì”…;
£®2£©»Ù![]() Œ™µ»—¸»˝Ω«–Œ£¨«Û¥À ±’˝∑Ω–Œ
Œ™µ»—¸»˝Ω«–Œ£¨«Û¥À ±’˝∑Ω–Œ![]() µƒ±ş≥§.
µƒ±ş≥§.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø÷–ª™Œƒ√˜£¨‘¥‘∂¡˜≥§£ª÷–ª™∫∫◊÷£¨‘¢“‚…Óπ„£ÆŒ™¡À¥´≥–÷–ª™√Ò◊”≈–„¥´Õ≥ŒƒªØ£¨Œ“ –ƒ≥÷–—ß柖–°∞∫∫◊÷Ã˝–¥°±±»»¸£¨»¸∫Û’˚¿Ì≤Œ»¸—ß…˙µƒ≥…º®£¨Ω´—ß…˙µƒ≥…º®∑÷Œ™A£¨B£¨C£¨DÀƒ∏ˆµ»º∂£¨≤¢Ω´Ω·π˚ªÊ÷∆≥…»ÁÕºÀ˘ 浃ÖŒÕ≥º∆Õº∫Õ…»–ŒÕ≥º∆Õº£¨µ´æ˘≤ªÕÍ’˚£Æ

«Îƒ„∏˘æıÕ≥º∆ÕºΩ‚¥œ¬¡–Œ £∫
£®1£©≤Œº”±»»¸µƒ—ß…˙π≤”–____√˚£ª
£®2£©‘Ğ…»–ŒÕ≥º∆Õº÷–£¨mµƒ÷µŒ™____£¨±Ì æ°∞Dµ»º∂°±µƒ…»–Œµƒ‘≤–ƒΩ«Œ™____∂»£ª
£®3£©◊Ȍت·æˆ∂®¥”±æ¥Œ±»»¸ªÒµ√Aµ»º∂µƒ—ß…˙÷–£¨—°≥ˆ2√˚»•≤Œº”»´ –÷–—ß…˙°∞∫∫◊÷Ã˝–¥°±¥Û»¸£Æ“—÷™Aµ»º∂—ß…˙÷–ƒ–…˙”–1√˚£¨«Î”√¡–±Ì∑®ªÚª≠ ˜◊¥Õº∑®«Û≥ˆÀ˘—°2√˚—ß…˙«°∫√ «“ª√˚ƒ–…˙∫Õ“ª√˚≈Æ…˙µƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ ±≥æ∞£∫»ÁÕº£¨Ω´![]() »∆µ„
»∆µ„![]() ƒÊ ±’Ζ˝◊™60°„µ√µΩ
ƒÊ ±’Ζ˝◊™60°„µ√µΩ![]() £¨
£¨![]() ”Î
”Î![]() Ωª”е„
Ωª”е„![]() £¨ø…Õ∆≥ˆΩ·¬ğ£∫
£¨ø…Õ∆≥ˆΩ·¬ğ£∫![]()
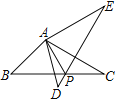
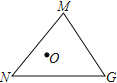
Œ Ã‚Ω‚æˆ£∫»ÁÕº£¨‘Ğ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £Æµ„
£Æµ„![]() «
«![]() ƒĞ“ªµ„£¨‘Úµ„
ƒĞ“ªµ„£¨‘Úµ„![]() µΩ
µΩ![]() »˝∏ˆ∂•µ„µƒæ‡¿Î∫Õµƒ◊Ó–°÷µ «___________
»˝∏ˆ∂•µ„µƒæ‡¿Î∫Õµƒ◊Ó–°÷µ «___________
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨æÿ–Œ![]() ÷–£¨
÷–£¨![]() ”Î
”Î![]() œ‡Ωª”е„
œ‡Ωª”е„![]() £¨
£¨![]() £¨Ω´
£¨Ω´![]() —ÿ
—ÿ![]() ’ğµ˛£¨µ„
’ğµ˛£¨µ„![]() µƒ∂‘”¶µ„Œ™
µƒ∂‘”¶µ„Œ™![]() £¨¡¨Ω”
£¨¡¨Ω”![]() Ωª
Ωª![]() ”е„
”е„![]() £¨«“
£¨«“![]() £¨‘Ğ
£¨‘Ğ![]() ±ş…œ”–“ªµ„
±ş…œ”–“ªµ„![]() £¨ πµ√
£¨ πµ√![]() µƒ÷µ◊Ó–°£¨¥À ±
µƒ÷µ◊Ó–°£¨¥À ±![]() £® £©
£® £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨µ»—¸
÷–£¨µ»—¸![]() µƒ±ş
µƒ±ş![]() ”Î∑¥±»¿˝∫Ø ˝
”Î∑¥±»¿˝∫Ø ˝![]() µƒÕºœÛœ‡Ωª”е„
µƒÕºœÛœ‡Ωª”е„![]() £¨∆‰÷–
£¨∆‰÷–![]() £¨µ„
£¨µ„![]() ‘Ğ
‘Ğ![]() ÷·µƒ’˝∞Î÷·…œ£¨µ„
÷·µƒ’˝∞Î÷·…œ£¨µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() ÷·”е„
÷·”е„![]() £Æ
£Æ
£®1£©“—÷™“ª¥Œ∫Ø ˝µƒÕºœÛπ˝µ„![]() £¨«Û∏√“ª¥Œ∫Ø ˝µƒ±Ì¥Ô Ω£ª
£¨«Û∏√“ª¥Œ∫Ø ˝µƒ±Ì¥Ô Ω£ª
£®2£©»Ùµ„![]() «œş∂Œ
«œş∂Œ![]() …œµƒ“ªµ„£¨¬˙◊„
…œµƒ“ªµ„£¨¬˙◊„![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() ÷·”е„
÷·”е„![]() £¨¡¨Ω·
£¨¡¨Ω·![]() £¨º«
£¨º«![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™![]() £¨…Ë
£¨…Ë![]() £¨
£¨![]() .
.
¢Ÿ”√![]() ±Ì æ
±Ì æ![]() £®≤ª–Ë“™–¥≥ˆ
£®≤ª–Ë“™–¥≥ˆ![]() µƒ»°÷µ∑∂Œß£©£ª
µƒ»°÷µ∑∂Œß£©£ª
¢Ğµ±![]() »°◊Ó–°÷µ ±£¨«Û
»°◊Ó–°÷µ ±£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒŞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com