
【题目】如图所示,在平面直角坐标系![]() 中,等腰
中,等腰![]() 的边
的边![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,其中
,其中![]() ,点
,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
(1)已知一次函数的图象过点![]() ,求该一次函数的表达式;
,求该一次函数的表达式;
(2)若点![]() 是线段
是线段![]() 上的一点,满足
上的一点,满足![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连结
,连结![]() ,记
,记![]() 的面积为
的面积为![]() ,设
,设![]() ,
,![]() .
.
①用![]() 表示
表示![]() (不需要写出
(不需要写出![]() 的取值范围);
的取值范围);
②当![]() 取最小值时,求
取最小值时,求![]() 的值.
的值.

科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ),
),![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求该抛物线的解析式,并写出它的对称轴;
(2)点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知![]() ,若
,若![]() 是抛物线上一个动点(其中
是抛物线上一个动点(其中![]() ),连接
),连接![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
(4)若点![]() 为抛物线对称轴上一点,抛物线上是否存在点
为抛物线对称轴上一点,抛物线上是否存在点![]() ,使得以
,使得以![]() 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点
为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动,为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育.科技.国防.农业.工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图,请根据图中所给的信息解答下列问题:
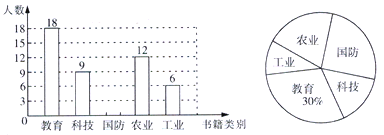
(1)在这次调查中,一共抽取了多少名学生?
(2)请通过计算补全条形统计图;
(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
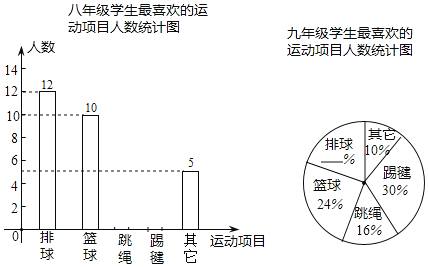
【题目】通辽市某中学为了了解学生“大课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 |
| 6 |
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取了多少人?
(2)补全统计表和统计图.
(3)该校有学生1800人,学校想对“最喜欢踢毽子”的学生每4人提供一个毽子,学校现有124个毽子,能否够用?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
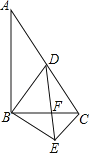
【题目】如图,在![]() 中,
中,![]() 为斜边
为斜边![]() 的中点,连接
的中点,连接![]() ,点
,点![]() 是
是![]() 边上的动点(不与点
边上的动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]() 延长线交于点
延长线交于点![]() ,连接
,连接![]() ,下列结论:
,下列结论:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③![]() 和
和![]() 一定相似;
一定相似;
④若![]() ,则
,则![]() .
.
其中正确的是_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农贸公司销售一批玉米种子,若一次购买不超过5千克,则种子价格为20元/千克,若一次购买超过5千克,则超过5千克部分的种子价格打8折.设一次购买量为x千克,付款金额为y元.
(1)求y关于x函数解析式;
(2)某农户一次购买玉米种子30千克,需付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,一同学利用直尺和圆规完成如下操作:
,一同学利用直尺和圆规完成如下操作:
①以点![]() 为圆心,以
为圆心,以![]() 为半径画弧,角
为半径画弧,角![]() 于点
于点![]() ;分别以点
;分别以点![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧交点
的长为半径画弧,两弧交点![]() ,作射线
,作射线![]() ;
;
②以点![]() 为圆心,以适当的长为半径画弧,交
为圆心,以适当的长为半径画弧,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ;分别以点
;分别以点![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,作直线
,作直线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交射线
,交射线![]() 于点
于点![]() .
.
请你观察图形,根据操作结果解答下列问题;
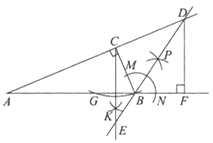
(1)线段![]() 与
与![]() 的大小关系是__________.
的大小关系是__________.
(2)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AC=BC,CD是⊙O的直径,与AB相交于点G,过点D作EF∥AB,分别交CA、CB的延长线于点E、F,连接BD.
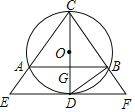
(1)求证:EF是⊙O的切线;
(2)求证:BD2=ACBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】思维启迪:(1)如图1,A,B两点分别位于一个池塘的两端,小亮想用绳子测量A,B间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达B点的点C,连接BC,取BC的中点P(点P可以直接到达A点),利用工具过点C作CD∥AB交AP的延长线于点D,此时测得CD=200米,那么A,B间的距离是 米.

思维探索:(2)在△ABC和△ADE中,AC=BC,AE=DE,且AE<AC,∠ACB=∠AED=90°,将△ADE绕点A顺时针方向旋转,把点E在AC边上时△ADE的位置作为起始位置(此时点B和点D位于AC的两侧),设旋转角为α,连接BD,点P是线段BD的中点,连接PC,PE.
①如图2,当△ADE在起始位置时,猜想:PC与PE的数量关系和位置关系分别是 ;
②如图3,当α=90°时,点D落在AB边上,请判断PC与PE的数量关系和位置关系,并证明你的结论;
③当α=150°时,若BC=3,DE=l,请直接写出PC2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com