
【题目】思维启迪:(1)如图1,A,B两点分别位于一个池塘的两端,小亮想用绳子测量A,B间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达B点的点C,连接BC,取BC的中点P(点P可以直接到达A点),利用工具过点C作CD∥AB交AP的延长线于点D,此时测得CD=200米,那么A,B间的距离是 米.

思维探索:(2)在△ABC和△ADE中,AC=BC,AE=DE,且AE<AC,∠ACB=∠AED=90°,将△ADE绕点A顺时针方向旋转,把点E在AC边上时△ADE的位置作为起始位置(此时点B和点D位于AC的两侧),设旋转角为α,连接BD,点P是线段BD的中点,连接PC,PE.
①如图2,当△ADE在起始位置时,猜想:PC与PE的数量关系和位置关系分别是 ;
②如图3,当α=90°时,点D落在AB边上,请判断PC与PE的数量关系和位置关系,并证明你的结论;
③当α=150°时,若BC=3,DE=l,请直接写出PC2的值.
【答案】(1)200;(2)①PC=PE,PC⊥PE;②PC与PE的数量关系和位置关系分别是PC=PE,PC⊥PE,见解析;③PC2=![]() .
.
【解析】
(1)由CD∥AB,可得∠C=∠B,根据∠APB=∠DPC即可证明△ABP≌△DCP,即可得AB=CD,即可解题.
(2)①延长EP交BC于F,易证△FBP≌△EDP(SAS)可得△EFC是等腰直角三角形,即可证明PC=PE,PC⊥PE.
②作BF∥DE,交EP延长线于点F,连接CE、CF,易证△FBP≌△EDP(SAS),结合已知得BF=DE=AE,再证明△FBC≌△EAC(SAS),可得△EFC是等腰直角三角形,即可证明PC=PE,PC⊥PE.
③作BF∥DE,交EP延长线于点F,连接CE、CF,过E点作EH⊥AC交CA延长线于H点,由旋转旋转可知,∠CAE=150°,DE与BC所成夹角的锐角为30°,得∠FBC=∠EAC,同②可证可得PC=PE,PC⊥PE,再由已知解三角形得∴EC2=CH2+HE2=![]() ,即可求出
,即可求出![]()
(1)解:∵CD∥AB,∴∠C=∠B,
在△ABP和△DCP中,
 ,
,
∴△ABP≌△DCP(SAS),
∴DC=AB.
∵AB=200米.
∴CD=200米,
故答案为:200.
(2)①PC与PE的数量关系和位置关系分别是PC=PE,PC⊥PE.
理由如下:如解图1,延长EP交BC于F,
同(1)理,可知∴△FBP≌△EDP(SAS),
∴PF=PE,BF=DE,
又∵AC=BC,AE=DE,
∴FC=EC,
又∵∠ACB=90°,
∴△EFC是等腰直角三角形,
∵EP=FP,
∴PC=PE,PC⊥PE.
②PC与PE的数量关系和位置关系分别是PC=PE,PC⊥PE.
理由如下:如解图2,作BF∥DE,交EP延长线于点F,连接CE、CF,
同①理,可知△FBP≌△EDP(SAS),
∴BF=DE,PE=PF=![]() ,
,
∵DE=AE,
∴BF=AE,
∵当α=90°时,∠EAC=90°,
∴ED∥AC,EA∥BC
∵FB∥AC,∠FBC=90,
∴∠CBF=∠CAE,
在△FBC和△EAC中,
 ,
,
∴△FBC≌△EAC(SAS),
∴CF=CE,∠FCB=∠ECA,
∵∠ACB=90°,
∴∠FCE=90°,
∴△FCE是等腰直角三角形,
∵EP=FP,
∴CP⊥EP,CP=EP=![]() .
.
③如解图3,作BF∥DE,交EP延长线于点F,连接CE、CF,过E点作EH⊥AC交CA延长线于H点,
当α=150°时,由旋转旋转可知,∠CAE=150°,DE与BC所成夹角的锐角为30°,
∴∠FBC=∠EAC=α=150°
同②可得△FBP≌△EDP(SAS),
同②△FCE是等腰直角三角形,CP⊥EP,CP=EP=![]() ,
,
在Rt△AHE中,∠EAH=30°,AE=DE=1,
∴HE=![]() ,AH=
,AH=![]() ,
,
又∵AC=AB=3,
∴CH=3+![]() ,
,
∴EC2=CH2+HE2=![]()
∴PC2=![]()





 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,等腰
中,等腰![]() 的边
的边![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,其中
,其中![]() ,点
,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
(1)已知一次函数的图象过点![]() ,求该一次函数的表达式;
,求该一次函数的表达式;
(2)若点![]() 是线段
是线段![]() 上的一点,满足
上的一点,满足![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连结
,连结![]() ,记
,记![]() 的面积为
的面积为![]() ,设
,设![]() ,
,![]() .
.
①用![]() 表示
表示![]() (不需要写出
(不需要写出![]() 的取值范围);
的取值范围);
②当![]() 取最小值时,求
取最小值时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,很多数学知识相互之间都是有联系的.如图,图一是“杨辉三角”数阵,其规律是:从第三行起,每行两端的数都是“1”,其余各数都等于该数“两肩”上的数之和;图二是二项和的乘方(a+b)n的展开式(按b的升幂排列).经观察:图二中某个二项和的乘方的展开式中,各项的系数与图一中某行的数一一对应,且这种关系可一直对应下去.将(s+x)15的展开式按x的升幂排列得:(s+x)15=a0+a1x+a2x2+…+a15x15

依上述规律,解决下列问题:(1)若s=1,则a2=___;(2)若s=2,则a0+a1+a2+…+a15=___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
x(元) | 15 | 20 | 30 | … |
y(袋) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数,试求:
(1)日销售量y(袋)与销售价x(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线经过点D(﹣2,﹣3)和点E(3,2),点P是第一象限抛物线上的一个动点.
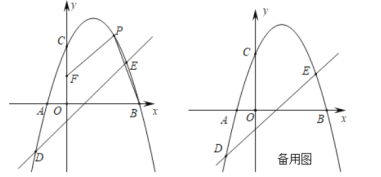
(1)求直线DE和抛物线的表达式;
(2)在y轴上取点F(0,1),连接PF,PB,当四边形OBPF的面积是7时,求点P的坐标;
(3)在(2)的条件下,当点P在抛物线对称轴的右侧时,直线DE上存在两点M,N(点M在点N的上方),且MN=2![]() ,动点Q从点P出发,沿P→M→N→A的路线运动到终点A,当点Q的运动路程最短时,请直接写出此时点N的坐标.
,动点Q从点P出发,沿P→M→N→A的路线运动到终点A,当点Q的运动路程最短时,请直接写出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F.已知AB=4,BC=6,CE=2,则CF的长等于( )
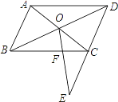
A. 1 B. 1.5 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
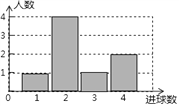
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度的变化是人们经常谈论的话题,请根据下图解决下列问题.
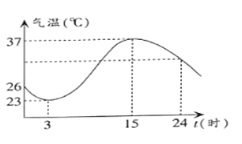
(1)这一天的最高温度是多少?是在几时到达的?
(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?
(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A(0,-2),B(-1,0),C(-5,0),点D从点B出发,沿x轴负方向运动到点C,E为AD上方一点,若在运动过程中始终保持△AED~△AOB,则点E运动的路径长为_______________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com