
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BCD=28°.
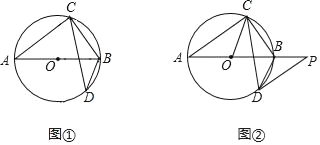
(I)如图①,求∠ABD的大小;
(Ⅱ)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
【答案】(I)∠ABD=62°;(Ⅱ)∠OCD=28°.
【解析】
(Ⅰ)根据圆周角定理可求∠ACB=90°,即可求∠ABD的度数;
(Ⅱ)根据切线的性质可得∠ODP=90°,且∠POD=2∠BCD=56°,即可求∠P=34°,根据平行线性质和等腰三角形的性质可求∠OCD的度数.
解:(Ⅰ)∵AB是直径,
∴∠ACB=90°,且∠BCD=28°,
∴∠ACD=62°,
∵∠ACD=∠ABD,
∴∠ABD=62°;
(Ⅱ)连接OD,
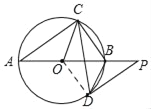
∵DP是⊙O的切线,
∴∠ODP=90°,
∵∠DOB=2∠DCB,
∴∠DOB=2×28°=56°,
∴∠P=34°,
∵AC∥DP,
∴∠P=∠OAC=34°,
∵OA=OC,
∴∠OAC=∠OCA=34°,
∴∠COB=∠OAC+∠OCA=68°,
∴∠COD=∠COB+∠DOB=124°
∵CO=DO
∴∠OCD=∠ODC=28°


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
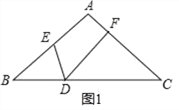
【题目】△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,求证:DECD=DFBE
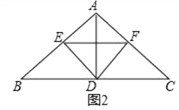
(2)D为BC中点如图2,连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
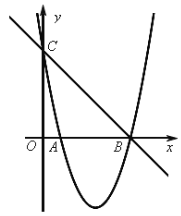
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有四个小球,球面上分别标有数字﹣2、0、1、2,它们除数字不同外没有任何区别,每次实验先搅拌均匀.
(1)从中任取一球,求抽取的数字为负数的概率;
(2)从中任取一球,将球上的数字记为x(不放回);再任取一球,将球上的数字记为y,试用画树状图(或列表法)表示所有可能出现的结果,并求“x+y>0”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c,当x=3时,y有最小值﹣4,且图象经过点(﹣1,12).
(1)求此二次函数的解析式;
(2)该抛物线交x轴于点A,B(点A在点B的左侧),交y轴于点C,在抛物线对称轴上有一动点P,求PA+PC的最小值,并求当PA+PC取最小值时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com