
【题目】已知二次函数y=ax2+bx+c,当x=3时,y有最小值﹣4,且图象经过点(﹣1,12).
(1)求此二次函数的解析式;
(2)该抛物线交x轴于点A,B(点A在点B的左侧),交y轴于点C,在抛物线对称轴上有一动点P,求PA+PC的最小值,并求当PA+PC取最小值时点P的坐标.
【答案】(1) y=x2﹣6x+5;(2) 当点P的坐标为(3,2)时,PA+PC取最小值,最小值为5![]() .
.
【解析】
(1)由顶点坐标将二次函数的解析式设成y=a(x-3)2-4,由该函数图象上一点的坐标,利用待定系数法即可求出二次函数的解析式;
(2)利用二次函数图象上点的坐标特征可求出点A、B、C的坐标,由二次函数图象的对称性可得出连接BC交抛物线对称轴于点P,此时PA+PC取最小值,最小值为BC,根据点B、C的坐标可求出直线BC的解析式及线段BC的长度,再利用一次函数图象上点的坐标特征即可求出点P的坐标,此题得解.
(1)∵当x=3时,y有最小值-4,
∴设二次函数解析式为y=a(x-3)2-4.
∵二次函数图象经过点(-1,12),
∴12=16a-4,
∴a=1,
∴二次函数的解析式为y=(x-3)2-4=x2-6x+5.
(2)当y=0时,有x2-6x+5=0,
解得:x1=1,x2=5,
∴点A的坐标为(1,0),点B的坐标为(5,0);
当x=0时,y=x2-6x+5=5,
∴点C的坐标为(0,5).
连接BC交抛物线对称轴于点P,此时PA+PC取最小值,最小值为BC,如图所示.
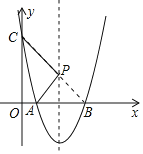
设直线BC的解析式为y=mx+n(m≠0),
将B(5,0)、C(0,5)代入y=mx+n,得:
![]() ,解得:
,解得:![]() ,
,
∴直线BC的解析式为y=-x+5.
∵B(5,0)、C(0,5),
∴BC=5![]() .
.
∵当x=3时,y=-x+5=2,
∴当点P的坐标为(3,2)时,PA+PC取最小值,最小值为5![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
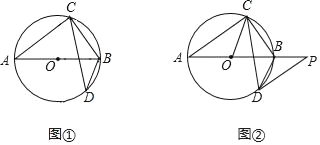
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BCD=28°.
(I)如图①,求∠ABD的大小;
(Ⅱ)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
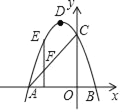
【题目】如图,在直角坐标系中,抛物线y=﹣(x+1)2+4与x轴交于点A、B,与y轴交于点C.
(1)写出抛物线顶点D的坐标 ;
(2)点D1是点D关于y轴的对称点,判断点D1是否在直线AC上,并说明理由;
(3)若点E是抛物线上的点,且在直线AC的上方,过点E作EF⊥x轴交线段AC于点F,求线段EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
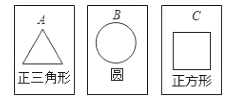
【题目】如图,有三张背面完全相同的纸牌A、B、C,其中正面分别画有三种不同的几何图形,小华将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张,请你用画树状图或列表的方法,求摸出的两张纸牌面上所画几何图形既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
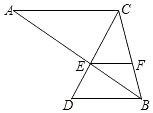
【题目】如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.
(1)求EF的长;
(2)如果△BEF的面积为4,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
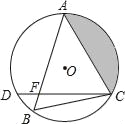
【题目】如图所示,在⊙O中,![]() ,弦CD与弦AB交于点F,连接BC,若∠ACD=60°,⊙O的半径长为2cm.
,弦CD与弦AB交于点F,连接BC,若∠ACD=60°,⊙O的半径长为2cm.
(1)求∠B的度数及圆心O到弦AC的距离;
(2)求图中阴影部分面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com