
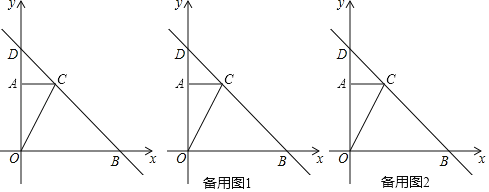
【题目】如图,在平面直角坐标系中,Rt△AOC的直角边OA在y轴正半轴上,且顶点O与坐标原点重合,点C的坐标为(1,2),直线y=﹣x+b过点C,与x轴交于点B,与y轴交于点D.
(1)B点的坐标为 ,D点的坐标为 ;
(2)动点P从点O出发,以每秒1个单位长度的速度,沿O→A→C的路线向点C运动,同时动点Q从点B出发,以相同速度沿BO的方向向点O运动,过点Q作QH⊥x轴,交线段BC或线段CO于点H.当点P到达点C时,点P和点Q都停止运动,在运动过程中,设动点P运动的时间为t秒:
①设△CPH的面积为S,求S关于t的函数关系式;
②是否存在以Q、P、H为顶点的三角形的面积与S相等?若存在,直接写出t的值;若不存在,请说明理由.
【答案】(1)(3,0);(0,3);(2)①S=  ;②存在,t=1或
;②存在,t=1或![]() 时,以Q、P、H为顶点的三角形的面积与S相等.
时,以Q、P、H为顶点的三角形的面积与S相等.
【解析】
(1)把点C坐标代入直线求得b的值即得到直线解析式,令y=0求点B坐标,令x=0求点D坐标.
(2)①由Rt△AOC中∠OAC=90°求得OA+AC=OB=3,即t的取值范围为0≤t<3且t≠2.画图发现有两种情况:当0≤t<2时,点P在线段OA上,点H在线段BC上,可证得PH∥x轴,故S=S△CPH=![]() PHAP,用t表示PH、AP的值再代入即能用t表示S;当2<t<3时,点P在线段AC上,点H在线段OC上,此时以PC为底、点H到CP距离h为高来求S,用t表示CP、h的值再代入即能用t表示S.再把两式统一写成S关于t的分段函数关系式.
PHAP,用t表示PH、AP的值再代入即能用t表示S;当2<t<3时,点P在线段AC上,点H在线段OC上,此时以PC为底、点H到CP距离h为高来求S,用t表示CP、h的值再代入即能用t表示S.再把两式统一写成S关于t的分段函数关系式.
②与①类似把点P、Q的位置分两种情况讨论计算;其中P在AC上、H在OC上时,以QH为底求△QPH的面积,需对点P到QH的距离PE的表示再进行一次分类.用t表示△QPH面积后与S相等列得方程,解之求得t的值.
解:(1)∵直线y=﹣x+b过点C(1,2)
∴﹣1+b=2
∴b=3,即直线为y=﹣x+3
当y=0时,﹣x+3=0,得x=3;当x=0时,y=3
∴B(3,0),D(0,3)
故答案为:(3,0);(0,3).
(2)①∵Rt△AOC中,∠OAC=90°,C(1,2)
∴A(0,2),OA=2,AC=1
∵OB=OD=3,∠BOD=90°
∴OA+AC=OB=3,∠OBD=45°
∴0≤t<3,且t≠2
i)当0≤t<2时,点P在线段OA上,点H在线段BC上,如图1
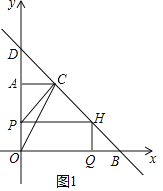
∴OP=BQ=t
∴AP=OA﹣OP=2﹣t,OQ=OB﹣BQ=3﹣t
∵HQ⊥x轴于点Q
∴∠BQH=90°
∴△BQH是等腰直角三角形
∴HQ=BQ=t
∴HQ∥OP且HQ=OP
∴四边形OPHQ是平行四边形
∴PH∥x轴,PH=OQ=3﹣t
∴S=S△CPH=![]() PHAP=
PHAP=![]() (3﹣
(3﹣![]() t2﹣
t2﹣![]() t+3
t+3
ii)当2<t<3时,点P在线段AC上,点H在线段OC上,如图2

∴CP=OA+AC﹣t=3﹣t,xH=OQ=3﹣t
∵直线OC解析式为:y=2x
∴QH=yH=2(3﹣t)=6﹣2t
∴点H到CP的距离h=2﹣(6﹣2t)=2t﹣4
∴S=S△CPH=![]() CPh=
CPh=![]() (3﹣t)(2t﹣4)=﹣t2+5t﹣6
(3﹣t)(2t﹣4)=﹣t2+5t﹣6
综上所述,S关于t的函数关系式为S= 
②存在以Q、P、H为顶点的三角形的面积与S相等.
i)当0≤t<2时,如图3
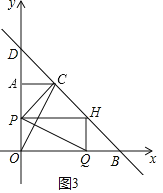
∵S△CPH=S△QPH,两三角形有公共底边为PH
∴点C和点Q到PH距离相等,即AP=OP
∴t=2﹣t
∴t=1
ii)当2<t≤2.5时,如图4,延长QH交AC于点E
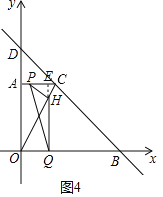
∴AE=OQ=3﹣t,AP=t﹣2,QH=6﹣2t
∴PE=AE﹣AP=(3﹣t)﹣(t﹣2)=5﹣2t
∴S△QPH=![]() QHPE=
QHPE=![]() (6﹣2t)(5﹣2t)=2t2﹣11t+15
(6﹣2t)(5﹣2t)=2t2﹣11t+15
∵S△CPH=S△QPH
∴﹣t2+5t﹣6=2t2﹣11t+15
解得:t1=3(舍去),t2=![]()
iii)当2.5<t<3时,如图5,延长QH交AC于点E

∴PE=AP﹣AE=(t﹣2)﹣(3﹣t)=2t﹣5
∴S△QPH=![]() QHPE=
QHPE=![]() (6﹣2t)(2t﹣5)=﹣2t2+11t﹣15
(6﹣2t)(2t﹣5)=﹣2t2+11t﹣15
∴﹣t2+5t﹣6=﹣2t2+11t﹣15
解得:t1=t2=3(舍去)
综上所述,t=1或![]() 时,以Q、P、H为顶点的三角形的面积与S相等.
时,以Q、P、H为顶点的三角形的面积与S相等.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图1,对角线互相垂直的四边形叫做垂美四边形.
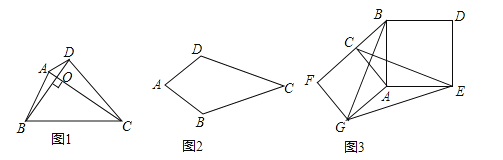
(1)概念理解:如图2,在四边形![]() 中,
中,![]() ,
,![]() ,问四边形
,问四边形![]() 是垂美四边形吗?请说明理由;
是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形![]() 的对角线
的对角线![]() 、
、![]() 交于点
交于点![]() ,
,![]() .试证明:
.试证明:![]() ;
;
(3)解决问题:如图3,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连结
,连结![]() 、
、![]() 、
、![]() .已知
.已知![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
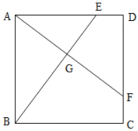
【题目】如图,正方形ABCD,点E,F分别在AD,CD上,且DE=CF,AF与BE相交于点G.
(1)求证:BE=AF;
(2)若AB=4,DE=1,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为拓展学生视野,促进书本知识与生活实践的深度融合,荆州市某中学组织八年级全体学生前往松滋洈水研学基地开展研学活动.在此次活动中,若每位老师带队14名学生,则还剩10名学生没老师带;若每位老师带队15名学生,就有一位老师少带6名学生,现有甲、乙两种大型客车,它们的载客量和租金如表所示:
甲型客车 | 乙型客车 | |
载客量(人/辆) | 35 | 30 |
租金(元/辆) | 400 | 320 |
学校计划此次研学活动的租金总费用不超过3000元,为安全起见,每辆客车上至少要有2名老师.
(1)参加此次研学活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆车上至少要有2名老师,可知租车总辆数为 辆;
(3)学校共有几种租车方案?最少租车费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△AOB的三个顶点A、O、B分别落在抛物线F1:![]() 的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
(1)求点A、B的坐标;
(2)将△AOB绕点O逆时针旋转90°得到△A'OB',抛物线F2:![]() 经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
(3)如图2,延长OB'交抛物线F2于点C,连接A'C,在坐标轴上是否存在点D,使得以A、O、D为顶点的三角形与△OA'C相似.若存在,请求出点D的坐标;若不存在,请说明理由.
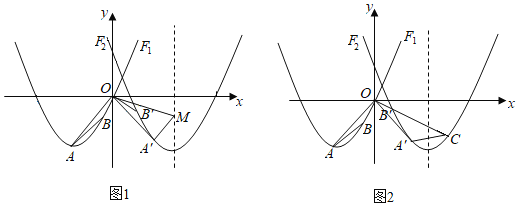
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]()
(1)请在网格中,画出线段![]() 关于原点对称的线段
关于原点对称的线段![]() ;
;
(2)请在网格中,过点![]() 画一条直线
画一条直线![]() ,将
,将![]() 分成面积相等的两部分,与线段
分成面积相等的两部分,与线段![]() 相交于点
相交于点![]() ,写出点
,写出点![]() 的坐标;
的坐标;
(3)若另有一点![]() ,连接
,连接![]() ,则
,则![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知⊙O外一点P向⊙O作切线PA,点A为切点,连接PO并延长交⊙O于点B,连接AO并延长交⊙O于点C,过点C作![]() ,分别交PB于点E,交⊙O于点D,连接AD.
,分别交PB于点E,交⊙O于点D,连接AD.

(1)求证:△APO~△DCA;
(2)如图2,当![]() 时
时
①求![]() 的度数;
的度数;
②连接AB,在⊙O上是否存在点Q使得四边形APQB是菱形.若存在,请直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
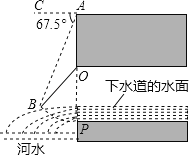
【题目】如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中OP为下水管道口直径,OB为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径OB=OP=100cm,OA为检修时阀门开启的位置,且OA=OB.
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达OB位置时,在点A处测得俯角∠CAB=67.5°,若此时点B恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
(![]() =1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
=1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个斜抛物体的水平运动距离为x(m),对应的高度记为h(m),且满足h=ax2+bx﹣11a(其中a≠0).已知当x=0时,h=2;当x=10时,h=2.
(1)求h关于x的函数表达式.
(2)求斜抛物体的最大高度和达到最大高度时的水平距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com