
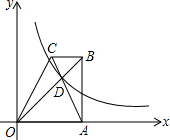
 如图,已知四边形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,对角线AC,BO相交于点D,反比例函数y=$\frac{k}{x}$经过点D.若△BCD的面积为3,△OCD的面积为6,则反比例函数的解析式为y=$\frac{16}{x}$.
如图,已知四边形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,对角线AC,BO相交于点D,反比例函数y=$\frac{k}{x}$经过点D.若△BCD的面积为3,△OCD的面积为6,则反比例函数的解析式为y=$\frac{16}{x}$. 分析 由△BCD的面积为3,△OCD的面积为6,得到$\frac{BD}{OD}$=$\frac{1}{2}$,根据△BCD∽△OAD,利用相似三角形的面积的比等于相似比的平方即可求得△OAD的面积,作DE⊥OA于点E,则DE∥AB,据此即可求得OE与OA的比值,根据三角形的面积公式即可求得△ODE的面积,根据反比例函数比例系数k的几何意义即可求解.
解答 解:作DE⊥OA于点E,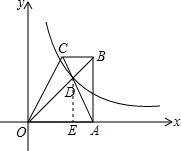
∵△BCD的面积为3,△OCD的面积为6,
∴$\frac{BD}{OD}$=$\frac{1}{2}$,
∵BC∥AO,
∴△BDC∽△AOD,
∴$\frac{{S}_{△BCD}}{{S}_{△OAD}}$=($\frac{BC}{OA}$)2=$\frac{1}{4}$,$\frac{OD}{BD}$=$\frac{OA}{BC}$=2,
∴S△OAD=12,
∵BC∥AO,
∴$\frac{OE}{AE}$=$\frac{OD}{BD}$=2,
∴OE=$\frac{2}{3}$OA,
∴S△ODE=$\frac{2}{3}$S△OAD=$\frac{2}{3}$×12=8,
∴k=16.
∴反比例函数的解析式为y=$\frac{16}{x}$,
故答案是:y=$\frac{16}{x}$.
点评 本题考查了相似三角形的性质以及反比例函数的几何意义,根据相似三角形的性质以及三角形的面积公式求得△ODE的面积是关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知∠AOB=60°,点P在边OA上,OP=20,点M,N在边OB上,PM=PN.若MN=6,则OM=( )
如图,已知∠AOB=60°,点P在边OA上,OP=20,点M,N在边OB上,PM=PN.若MN=6,则OM=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商场有一个可以自由转动的转盘(如图),规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某商场有一个可以自由转动的转盘(如图),规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
| 落在“铅笔”的频率$\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com