
【题目】如图,在△ABC中,△ABC的角平分线OB与角平分线OC相交于点O,过点O作MN∥BC,分别交AB、AC于点M、N.

(1)请写出图中所有的等腰三角形;
(2)若AB+AC=14,求△AMN的周长.
【答案】(1)△MBO和△NOC是等腰三角形;(2)14
【解析】
试题分析:(1)由OB平分∠ABC,得到∠MBO=∠OBC,根据平行线的性质得到∠MOB=∠OBC,等量代换得到∠MBO=∠MOB,于是得到结论;
(2)由OB平分∠ABC,得到∠MBO=∠OBC,根据平行线的性质得到∠MOB=∠OBC,等量代换得到∠MBO=∠MOB,得到MO=MB,同理可证:ON=NC,根据周长的计算公式得到结论.
解:(1)△MBO和△NOC是等腰三角形,
∵OB平分∠ABC,
∴∠MBO=∠OBC,
∵MN∥BC,
∴∠MOB=∠OBC,
∴∠MBO=∠MOB,
∴MO=MB,
同理可证:ON=NC,
∴△MBO和△NOC是等腰三角形;
(2)∵OB平分∠ABC,
∴∠MBO=∠OBC,
∵MN∥BC,
∴∠MOB=∠OBC,
∴∠MBO=∠MOB,
∴MO=MB,
同理可证:ON=NC,
∵△AMN的周长=AM+MO+ON+AN,
∴△AMN的周长=AM+MB+AN+NC=AB+AC=14.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,把∠B,∠D分别翻折,使点B,D分别落在对角线AC上的点E,F处,折痕分别为CM,AN.
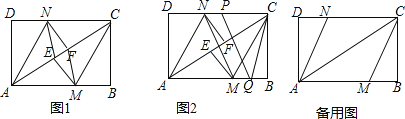
(1)求证:△AND≌△CMB;
(2)连接MF、NE,证明四边形MFNE是平行四边形;四边形MFNE是菱形吗?请说明理由;
(3)点P、Q是矩形的边CD、AB上的两点,连接PQ、CQ、MN,如图2所示,若PQ=CQ,PQ∥MN,且AB=4,BC=3,DN=![]() ,求PC的长度.
,求PC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自北京成功举办2008年夏季奥运会,去年又成功获得2022年冬季奥运会举办权以来,奥运知识在我国不断传播.小刚就本班学生的对奥运知识的了解程度进行了一次调查统计.A:熟悉,B:了解较多,C:一般了解.图25-1和图25-2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:

(1)该班共有 名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整.
(3)在扇形统计图中,“了解较多”部分所对应的圆心角的度数为 ;
(4)如果全年级共1000名同学,请你估算全年级对奥运知识 “了解较多”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
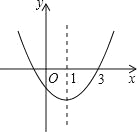
A.4ac﹣b2<0 B.a﹣b+c<0 C.2a+b<0 D.abc<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程x2+px+q=0的两根分别为X1=2,X2=-1,那么p,q的值分别是 ( )
A.1-,2
B.-1,-2
C.-1,2
D.1,2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,采取分段收费.若每户每月用水量不超过20 m3,每立方米收费2元;若用水量超过20 m3,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com