
【题目】某淘宝网店销售台灯,成本为每个30元.销售大数据分析表明:当每个台灯售价为40元时,平均每月售出600个;若售价每下降1元,其月销售量就增加200个.
(1)若售价下降1元,每月能售出 个台灯,若售价下降x元(![]() ),每月能售出 个台灯.
),每月能售出 个台灯.
(2)为迎接“双十一”,该网店决定降价促销,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.
(3)月获利能否达到9600元,说明理由.
【答案】(1)800;600+200x;(2)每个台灯的售价为37元;(3)月获利不能达到9600元,理由见解析.
【解析】
(1)根据售价每下降1元,其月销售量就增加200个,分别计算即可;
(2)设每个台灯的售价为x元,根据每个台灯的利润×销售数量=总利润列出方程并解答;
(3)根据题意列出方程,求出根的判别式△<0,可得方程无实数根,即月获利不能达到9600元.
解:(1)∵售价每下降1元,其月销售量就增加200个,
∴若售价下降1元,每月能售出600+200=800个台灯,若售价下降x元(![]() ),每月能售出600+200x个台灯;
),每月能售出600+200x个台灯;
(2)设每个台灯的售价为x元,
由题意得:(x-30)[600+200(40-x)]=8400,
解得:x1=36,x2=37,
当x=36时,600+200(40-x)=1400>1210(舍去),
当x=37时,600+200(40-x)=1200<1210(符合题意),
答:每个台灯的售价为37元;
(3)月获利不能达到9600元,
理由:设每个台灯的售价为x元,
由题意得:(x-30)[600+200(40-x)]=9600,
整理得:x2-73x+1338=0,
∵△=b2-4ac=-23<0,
∴方程无实数根,即月获利不能达到9600元.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
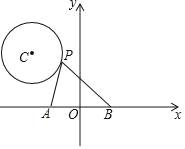
【题目】如图,在平面直角坐标系中,点P是以C(﹣![]() ,
,![]() )为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是_____.
)为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校举办的“弘扬社会主义核心价值观”为主题的演讲比赛中,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南京某特产专卖店的销售某种特产,其进价为每千克40元,若按每千克60元出售,则平均每天可售出100千克,后来经过市场调查发现,单价每降低3元,平均每天的销售量增加30千克,若专卖店销售这种特产想要平均每天获利2240元,且销量尽可能大,则每千克特产应定价多少元?
(1)方法1:设每千克特产应降价x元,由题意,得方程为:___.
方法2:设每千克特产降价后定价为x元,由题意,得方程为:___.
(2)请你选择一种方法完成解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,![]() =
=![]() ,BE交AD于点F.
,BE交AD于点F.
(1)∠ACB与∠BAD相等吗?为什么?
(2)判断△FAB的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
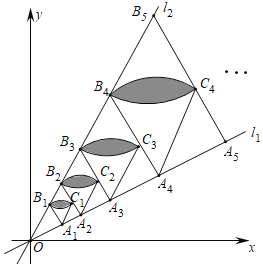
【题目】如图,直线l1的解析式是![]() ,直线l2的解析式是
,直线l2的解析式是![]() ,点A1在l1上,A1的横坐标为
,点A1在l1上,A1的横坐标为![]() ,作
,作![]() 交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则
交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则![]() ________.(用含有正整数n的式子表示)
________.(用含有正整数n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
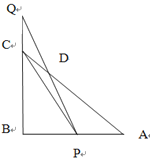
【题目】如图,等腰Rt△ABC的直角边AB=2,点P、Q分别从A、C两点同时出发,以相等的速度作直线运动,已知点P沿射线AB运动,点Q沿边BC的延长线运动,PQ与直线相交于点D.
(1)设AP的长为x,△PCQ的面积为S,求出S关于x的函数关系式;
(2)当AP的长为何值时,![]() =
=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com