
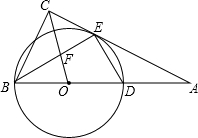
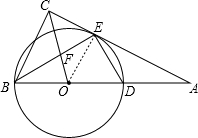
如图,在Rt△ABC中,∠ACB=90°,以斜边AB上一点O为圆心,OB为半径作⊙O,交AC于点E,交AB于点D,且∠BEC=∠BDE.
(1)求证:AC是⊙O的切线;
(2)连接OC交BE于点F,若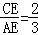 ,求
,求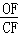 的值.
的值.
【考点】切线的判定;相似三角形的判定与性质.
【分析】(1)连接OE,证得OE⊥AC即可确定AC是切线;
(2)根据OE∥BC,分别得到△AOE∽△ACB和△OEF∽△CBF,利用相似三角形对应边的比相等找到中间比即可求解.
【解答】解:(1)证明:连接OE,
∵OB=OE,
∴∠OBE=∠OEB,
∵∠ACB=90°,
∴∠CBE+∠BEC=90°,
∵BD为⊙O的直径,
∴∠BED=90°,
∴∠DBE+∠BDE=90°,
∴∠CBE=∠DBE,
∴∠CBE=∠OEB,
∴OE∥BC,
∴∠OEA=∠ACB=90°,
即OE⊥AC,
∴AC为⊙O的切线;
(2)∵OE∥BC,∴△AOE∽△ABC,
∴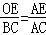 ,
,
∵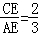 ,
,
∴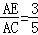 ,
,
∴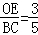 ,
,
∵OE∥BC,
∴△OEF∽△CBF,
∴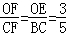 .
.
【点评】本题考查了切线的性质及判断,在解决切线问题时,常常连接圆心和切点,证明垂直或根据切线得到垂直.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
已知 :如图,△ABC中,∠C=90°,学习等边三角形时,我们知道,如果∠A=30°,那么AB=2BC,由此我们猜想,如果AB=2BC,那么∠A=30°,请你利用轴对称变换,证明这个结论.
:如图,△ABC中,∠C=90°,学习等边三角形时,我们知道,如果∠A=30°,那么AB=2BC,由此我们猜想,如果AB=2BC,那么∠A=30°,请你利用轴对称变换,证明这个结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
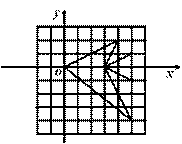
将如图各点纵坐标不变,横坐标乘以2,所得图形与原图形比( )
A.形状大小变了,整体鱼被横向拉长为原来的2倍
B.形状大小变了,整体鱼被纵向拉长为原来的2倍
C.形状大小不变 ,整体鱼向右移动了两个单位
,整体鱼向右移动了两个单位
D.形状大小不变,整体鱼向左移动了两个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
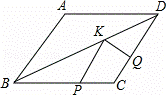
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为
A. 2 B. 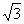
C. 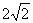 D.
D.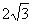
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com