
����Ŀ��ijУΪ�˽�ѧ���Ŀ����Ķ��������������˲���ѧ��ƽ��ÿ��Ŀ����Ķ�ʱ�䣬�����ݵ������Ƴɱ�����ѧ��������ͳ��ͼ�����£�����Ϣ��������
ʱ��(Сʱ) | 0.5 | 1 | 1.5 | 2 |
���� | 2 | 5 | 3 |
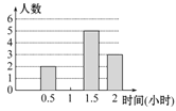
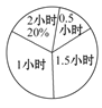
��������ṩ��Ϣ������������⣺
��1��������ͳ��ͼ�У�����ʱ��Ϊ��2Сʱ�����ֵ�Բ�ĽǵĶ�����
��2��ͨ���������ȫУÿ��ѧ��ƽ��ÿ��Ŀ����Ķ�ʱ�䣮
��3���ӱ�����Ŀ������ʱ�����ٺ�����ѧ���У������2��ѧ�����з�̸������鵽1�˵ĸ��ʣ�
���𰸡���1��72������2��1.3Сʱ����3��![]()
��������
��1����360�������Ķ�ʱ��Ϊ2Сʱ�IJ�����ռ�ı������ɣ�
��2�������������ѧ��������������Ķ�ʱ��Ϊ1Сʱ���������������������ѧ���Ŀ����Ķ�ʱ�䣬�ݴ˹��ƿ�ȫУÿ��ѧ��ƽ��ÿ��Ŀ����Ķ�ʱ�䣮
��3�����б����һ���ж����ֵȿ��ܵĽ���������鵽1���м��ֽ��������ȷ�����鵽1�˵ĸ��ʣ�
��1�����Ķ�ʱ��Ϊ2Сʱ������ռ20%��
����Բ�Ľ�Ϊ360���20%=72����
��2�����Ķ�ʱ��Ϊ2Сʱ������Ϊ3�ˣ�ռ20%��
�౻����ѧ������Ϊ![]() =15��
=15��
���Ķ�ʱ��Ϊ1Сʱ������Ϊ15-(2+5+3)=5����ÿ��ѧ������ƽ���Ķ�ʱ��Ϊ��
![]() (Сʱ)
(Сʱ)
�����ȫУÿ��ѧ��ƽ��ÿ��Ŀ����Ķ�ʱ��Ϊ1.3Сʱ��
��3�����Ķ�ʱ�����ٵ�2��ΪA1��A2���Ķ�ʱ������3��ΪB1��B2��B3���б�Ϊ��
�ڶ����� ��һ���� | A1 | A2 | B1 | B2 | B3 |
A1 | �D | (A1A2) | (A1B1) | (A1B2) | (A1B3) |
A2 | (A2A1) | �D | (A2B1) | (A2B2) | (A2B3) |
B1 | (B1A1) | (B1A2) | �D | (B1B2) | (B1B3) |
B2 | (B2A1) | (B2A2) | (B2B1) | �D | (B2B3) |
B3 | (B3A1) | (B3A2) | (B3B1) | (B3B2) | �D |
����20�ֵȿ��ܵĽ�������и��鵽1�˵ij鷨��12�֣�����鵽1�˵ĸ���![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��sin��C![]() ������Ϊ2���߶�ED������CF�ϻ�������B������CA�ϣ���BC=5�����BDE�ܳ�����СֵΪ______��
������Ϊ2���߶�ED������CF�ϻ�������B������CA�ϣ���BC=5�����BDE�ܳ�����СֵΪ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
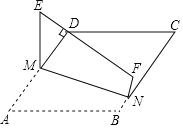
����Ŀ����ͼ��������ABCD�У�tanA��![]() ��M��N�ֱ��ڱ�AD��BC�ϣ����ı���AMNB��MN���ۣ�ʹAB�Ķ�Ӧ�߶�EF��������D����EF��ADʱ��
��M��N�ֱ��ڱ�AD��BC�ϣ����ı���AMNB��MN���ۣ�ʹAB�Ķ�Ӧ�߶�EF��������D����EF��ADʱ��![]() ��ֵΪ��������
��ֵΪ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺ѧϰ�˶��θ�ʽ����ᷢ��һЩ���и��ŵ�ʽ�ӿ���д����һ��ʽ�ӵ�ƽ������3+2![]() ����1+
����1+![]() ��2���������������µ�̽����
��2���������������µ�̽����
��a+b![]() ����m+n
����m+n![]() ��2������a��b��m��n������������������a+b
��2������a��b��m��n������������������a+b![]() ��m2+2n2+2mn
��m2+2n2+2mn![]() ����a��m2+2n2��b��2mn�������͵ó��˰�����a+b
����a��m2+2n2��b��2mn�������͵ó��˰�����a+b![]() ��ʽ�ӻ�Ϊƽ��ʽ�ķ������������������̽��������������⣺
��ʽ�ӻ�Ϊƽ��ʽ�ķ������������������̽��������������⣺
��1����a��b��m��n��Ϊ������ʱ����a+b![]() ����m+n
����m+n![]() ��2���ú�m��n��ʽ�ӷֱ��ʾa��b����a���� ����b���� ����
��2���ú�m��n��ʽ�ӷֱ��ʾa��b����a���� ����b���� ����
��2����a��4![]() ����m��n
����m��n![]() ��2��a��m��n��Ϊ����������a��ֵ��
��2��a��m��n��Ϊ����������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
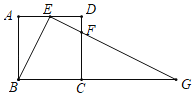
����Ŀ����ͼ����������ABCD�У�EΪ��AD���е㣬��F�ڱ�CD�ϣ��ҡ�BEF��90�����ӳ�EF��BC���ӳ����ڵ�G.
(1)��֤����ABE�ס�EGB.
(2)��AB��4����CG�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
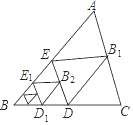
����Ŀ����ͼ��ʾ�����ɱ���������ѧ�Ҵ��Ļ���ݻ����ɵ�ͼ���������岿������һ�����ĵ���ֱ���������������Ӷ��ɣ����С�MA1A2����MA2A3������MAnAn+1��90������nΪ������������M��������ǣ���1��2����A1�������ǣ�0��2������A22������Ϊ��������

A.����1��29��2��29��B.��1��29��2��29��
C.����1��210��2��210��D.��1��210��2��210��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ڽ��ڡ�O��CA��CB������A��AE��BC������O�ڵ�E������C����O�����߽�AE���ӳ����ڵ�D����֪AB��6��BE��3![]() ��
��
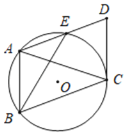
��1����֤���ı���ABCDΪƽ���ı��Σ�
��2���ӳ�AO��DC���ӳ����ڵ�F����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ҫ��Ӫһ�������е��ľߣ�����Ϊ20Ԫ����Ӫ���η��֣������۵�����25Ԫʱ��ÿ���������Ϊ250�������۵���ÿ����1Ԫ��ÿ����������ͼ���10��
��1��д���̳����������ľߣ�ÿ�����õ���������![]() ��Ԫ�������۵���
��Ԫ�������۵���![]() ��Ԫ��֮��ĺ�����ϵʽ��
��Ԫ��֮��ĺ�����ϵʽ��
��2�������۵���Ϊ����Ԫʱ�����ľ�ÿ��������������
��3���̳���Ӫ���������������������A��B����Ӫ������
����A�����ľߵ����۵��۸��ڽ����Ҳ�����30Ԫ��
����B��ÿ��������������10������ÿ���ľߵ���������Ϊ25Ԫ
��Ƚ����ַ��������������ߣ���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ���Ź�
���Ź�![]() ���е�
���е�![]() ��ֱ���۵���ʹ��
��ֱ���۵���ʹ��![]() ����
����![]() ���ϵ�
���ϵ�![]() ������Ϊ��һ�β������ۺ�
������Ϊ��һ�β������ۺ�![]() ��
��![]() �ľ���Ϊ
�ľ���Ϊ![]() ����ԭֽƬ���ٽ�
����ԭֽƬ���ٽ�![]() ���Ź�
���Ź�![]() ���е�
���е�![]() ��ֱ���۵���ʹ��
��ֱ���۵���ʹ��![]() ����
����![]() ���ϵ�
���ϵ�![]() ������Ϊ�ڶ��β������ۺ�
������Ϊ�ڶ��β������ۺ�![]() ��
��![]() �ľ����Ϊ
�ľ����Ϊ![]() ���������������ϲ�����ȥ����������
���������������ϲ�����ȥ����������![]() �β�����õ��ۺ�
�β�����õ��ۺ�![]() ����
����![]() �ľ����Ϊ
�ľ����Ϊ![]() ����
����![]() ����
����![]() ��ֵΪ��������
��ֵΪ��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com