
 如图,在△ABC中,∠C=90°,AC=BC=4,CD=1,点E为斜边AB上动点,连接CE、DE,则△CDE周长的最小值是6.
如图,在△ABC中,∠C=90°,AC=BC=4,CD=1,点E为斜边AB上动点,连接CE、DE,则△CDE周长的最小值是6. 分析 如图,作点C关于AB的对称点M,连接DM与AB交于点E,此时EC+ED最小,且EC+ED=EM+DE=DM,只要证明△MBD是直角三角形即可解决问题.
解答 解:如图 ,作点C关于AB的对称点M,连接DM与AB交于点E,此时EC+ED最小,连接BM.
,作点C关于AB的对称点M,连接DM与AB交于点E,此时EC+ED最小,连接BM.
∵∠ACB=90°,AC=CB=4,CD=1,
∴∠A=∠ABC=45°,DB=BC-CD=3,
∵C、M关于AB对称,
∴BM=BC=4,∠ABM=∠ABC=45°,EC=EM,
∴∠MBD=90°,
∴EC+ED=EM+ED=DM=$\sqrt{B{D}^{2}+B{M}^{2}}$=$\sqrt{{3}^{2}{+4}^{2}}$=5.
∴△CDE的周长为5+1=6.
故答案为6.
点评 本题考查最短问题、等腰直角三角形的性质、勾股定理等知识,解题的关键是利用对称确定最值,需要正确画图找到点E的位置,最后利用勾股定理求出最小值,这里体现了转化的思想,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知△ABC中,∠ABC为钝角.请你按要求作图(不写作法,但要保留作图痕迹):
已知△ABC中,∠ABC为钝角.请你按要求作图(不写作法,但要保留作图痕迹):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
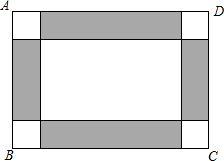 暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.
暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
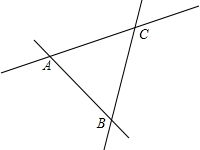 如图所示,三条公路分别相交于A、B、C三点,现计划修建一个加油站,要求该加油站到三条公路的距离相等,用直尺和圆规作出加油站O的位置.(不写作法,请保留作图痕迹)
如图所示,三条公路分别相交于A、B、C三点,现计划修建一个加油站,要求该加油站到三条公路的距离相等,用直尺和圆规作出加油站O的位置.(不写作法,请保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A=2∠B=3∠C | B. | ∠A+∠B=2∠C | C. | ∠A=∠B=30° | D. | ∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com