
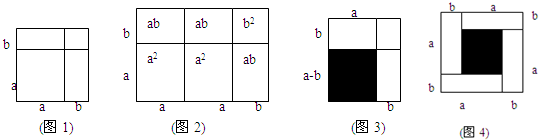
分析 问题一:
(1)根据图形面积可以得出公式;
(2)根据面积关系可以得出公式(a-b)2=a2-2ab+b2;
问题二:
(1)根据图形面积可以得出;
(2)利用图4的阴影的面积公式,代入a+b=7,a-b=4,求出ab即可.
解答 解:问题一:
(1)2a2+3ab+b2=(a+b)(2a+b),
(2)(a-b)2=a2-2ab+b2;
问题二:
(1)图3为:(a-b)2=a2-2ab+b2;图4为:(a-b)2=(a+b)2-4ab;
(2)由图4可知:(a-b)2=(a+b)2-4ab;
∵a+b=7,a-b=4,
∴42=72-4ab,
∴ab=$\frac{33}{4}$,
故一个小长方形的面积为$\frac{33}{4}$.
点评 此题考查了对完全平方公式几何意义的理解,应从整体和部分两方面来理解完全平方公式的几何意义;主要围绕图形面积展开分析.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )
如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
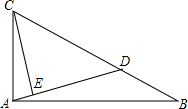 如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{2}$,BC=3BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{4}$.
如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{2}$,BC=3BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
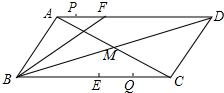 如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动.点P运动到F点时停止运动,点Q也同时停止运动.当点P运动3或5秒时,以点P、Q、E、F为顶点的四边形是平行四边形.
如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动.点P运动到F点时停止运动,点Q也同时停止运动.当点P运动3或5秒时,以点P、Q、E、F为顶点的四边形是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
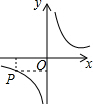 如图,双曲线上任意点P,向x、y轴分别作垂线围成的矩形面积为2,那么反比例函数的解析式是( )
如图,双曲线上任意点P,向x、y轴分别作垂线围成的矩形面积为2,那么反比例函数的解析式是( )| A. | y=$\frac{1}{x}$ | B. | y=$\frac{2}{x}$ | C. | y=-$\frac{1}{x}$ | D. | y=-$\frac{2}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
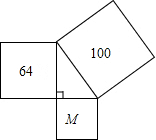 如图,三个正方形围成一个直角三角形,64、100分别为所在正方形的面积,则图中字母所代表的正方形的边长是( )
如图,三个正方形围成一个直角三角形,64、100分别为所在正方形的面积,则图中字母所代表的正方形的边长是( )| A. | 36 | B. | $4\sqrt{41}$ | C. | 6 | D. | 164 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为迎接市教育局开展的“学雷锋•做有道德的人”主题演讲活动,某区教育局团委组织各校学生进行演讲预赛,然后将所有参赛学生的成绩(得分为整数,满分为100分)分成四组,绘制了不完整的统计图表如下:
为迎接市教育局开展的“学雷锋•做有道德的人”主题演讲活动,某区教育局团委组织各校学生进行演讲预赛,然后将所有参赛学生的成绩(得分为整数,满分为100分)分成四组,绘制了不完整的统计图表如下:| 组别 | 成绩x | 组中值 | 频数 |
| 第一组 | 90≤x≤100 | 95 | 4 |
| 第二组 | 80≤x<90 | 85 | 10 |
| 第三组 | 70≤x<80 | 75 | 8 |
| 第四组 | 60≤x<70 | 65 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com