
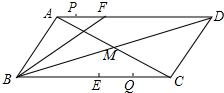
 如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动.点P运动到F点时停止运动,点Q也同时停止运动.当点P运动3或5秒时,以点P、Q、E、F为顶点的四边形是平行四边形.
如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动.点P运动到F点时停止运动,点Q也同时停止运动.当点P运动3或5秒时,以点P、Q、E、F为顶点的四边形是平行四边形. 分析 由四边形ABCD是平行四边形得出:AD∥BC,AD=BC,∠ADB=∠CBD,证得FB=FD,求出AD的长,得出CE的长,设当点P运动t秒时,点P、Q、E、F为顶点的四边形是平行四边形,根据题意列出方程并解方程即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADB=∠CBD,
∵∠FBM=∠CBM,
∴∠FBD=∠FDB,
∴FB=FD=12cm,
∵AF=6cm,
∴AD=18cm,
∵点E是BC的中点,
∴CE=$\frac{1}{2}$BC=$\frac{1}{2}$AD=9cm,
要使点P、Q、E、F为顶点的四边形是平行四边形,则PF=EQ即可,
设当点P运动t秒时,点P、Q、E、F为顶点的四边形是平行四边形,
根据题意得:6-t=9-2t或6-t=2t-9,
解得:t=3或t=5.
点评 本题考查了平行四边形的判定与性质、等腰三角形的判定与性质、一元一次方程的应用等知识,熟练掌握平行四边形的判定与性质是解决问题的关键.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
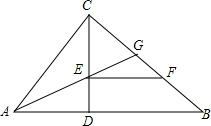 如图,△ABC中,∠ACB=90°,CD是高,AG平分∠CAB,EF∥AB,AC=6,BC=8.
如图,△ABC中,∠ACB=90°,CD是高,AG平分∠CAB,EF∥AB,AC=6,BC=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
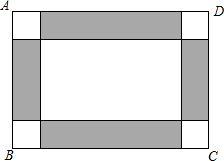 暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.
暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知抛物线y=ax2+bx+3与x轴交于点A(-3,0),B(1,0),P是其对称轴上的一个动点,连接PB、PC,下列结论:①2a+b>-$\frac{3}{2}$;②对称轴是直线x=-1;③当y=3时,x=0;④PB+PC的最小值是3$\sqrt{2}$.其中正确的有( )
如图,已知抛物线y=ax2+bx+3与x轴交于点A(-3,0),B(1,0),P是其对称轴上的一个动点,连接PB、PC,下列结论:①2a+b>-$\frac{3}{2}$;②对称轴是直线x=-1;③当y=3时,x=0;④PB+PC的最小值是3$\sqrt{2}$.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com