
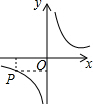
 如图,双曲线上任意点P,向x、y轴分别作垂线围成的矩形面积为2,那么反比例函数的解析式是( )
如图,双曲线上任意点P,向x、y轴分别作垂线围成的矩形面积为2,那么反比例函数的解析式是( )| A. | y=$\frac{1}{x}$ | B. | y=$\frac{2}{x}$ | C. | y=-$\frac{1}{x}$ | D. | y=-$\frac{2}{x}$ |
科目:初中数学 来源: 题型:解答题
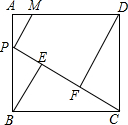 如图,P为正方形ABCD的边AB上的一个动点(点P不与A、B重合),连结PC,作BE⊥PC,DF⊥PC,垂足分别为点E、F,已知AD=5.
如图,P为正方形ABCD的边AB上的一个动点(点P不与A、B重合),连结PC,作BE⊥PC,DF⊥PC,垂足分别为点E、F,已知AD=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
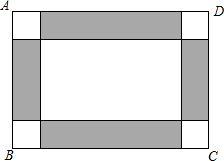 暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.
暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-2)2=1 | B. | (x-2)2=9 | C. | (x-4)2=21 | D. | (x-4)2=11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=5}\\{{x}^{2}-1=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2(x-y)=1}\\{3x=2-4y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=1}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=\frac{1}{x}}\\{x-y=2}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com