
分析 因为已知长度为4cm和9cm两边,没有明确是底边还是腰,所以有两种情况,需要分类讨论.
根据题意画出图形,进而利用勾股定理得出答案.
解答 解:①当4cm为底时,其它两边都为9cm,
4cm、8cm、8cm可以构成三角形,
周长为20cm;
②当4cm为腰时,
其它两边为4cm和9cm,
∵4+4<9,
∴不能构成三角形,故舍去.
∴这个等腰三角形的周长为20cm.
故答案为:20.
如图所示:等腰三角形一腰长为5,一边上的高为3,
则AB=5,AD=3,故BD=$\sqrt{{5}^{2}-{3}^{2}}$=4,
则底边长为:8.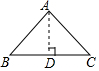 .
.
故答案为:8.
点评 此题主要考查了勾股定理以及等腰三角形的性质,正确应用勾股定理是解题关键.


科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌(元) | +2 | -0.5 | +1.5 | -1.8 | +0.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点P1在四边形ABCD的内部,点P2在边CD上,直线l在四边形ABCD外.
如图,点P1在四边形ABCD的内部,点P2在边CD上,直线l在四边形ABCD外.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校八年级全体320名学生在电脑培训前、后分别参加了一次水平相同的考试,考分都以同一标准划分成“不合格”“合格”“优秀”三个等级,为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示,试结合图示信息回答下列问题:
某校八年级全体320名学生在电脑培训前、后分别参加了一次水平相同的考试,考分都以同一标准划分成“不合格”“合格”“优秀”三个等级,为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示,试结合图示信息回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com