
°Њћвƒњ°њ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђќ“√«ґ®“е÷±ѕяy=ax-aќ™≈„ќпѕяy=ax2+bx+c£®a°Ґb°Ґcќ™≥£ э£ђa°ў0£©µƒ°∞—№…ъ÷±ѕя°±£ї”–“їЄцґ•µг‘Џ≈„ќпѕя…ѕ£ђЅн”–“їЄцґ•µг‘Џy÷б…ѕµƒ»эљ«–ќќ™∆д°∞—№…ъ»эљ«–ќ°±£Ѓ“—÷™≈„ќпѕя![]() ”л∆д°∞—№…ъ÷±ѕя°±љї”ЏA°ҐBЅљµг£®µгA‘ЏµгBµƒ„у≤а£©£ђ”лx÷бЄЇ∞л÷бљї”ЏµгC£Ѓ
”л∆д°∞—№…ъ÷±ѕя°±љї”ЏA°ҐBЅљµг£®µгA‘ЏµгBµƒ„у≤а£©£ђ”лx÷бЄЇ∞л÷бљї”ЏµгC£Ѓ
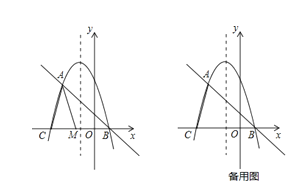
£®1£©ћоњ’£ЇЄ√≈„ќпѕяµƒ°∞—№…ъ÷±ѕя°±µƒљвќц љќ™ £ђµгAµƒ„ш±кќ™ £ђµгBµƒ„ш±кќ™ £ї
£®2£©»зЌЉ£ђµгMќ™ѕяґќCB…ѕ“їґѓµг£ђљЂ°чACM“‘AMЋщ‘Џ÷±ѕяќ™ґ‘≥∆÷бЈ≠’џ£ђµгCµƒґ‘≥∆µгќ™N£ђ»ф°чAMNќ™Є√≈„ќпѕяµƒ°∞—№…ъ»эљ«–ќ°±£ђ«уµгNµƒ„ш±к£ї
£®3£©µ±µгE‘Џ≈„ќпѕяµƒґ‘≥∆÷б…ѕ‘Ћґѓ ±£ђ‘ЏЄ√≈„ќпѕяµƒ°∞—№…ъ÷±ѕя°±…ѕ£ђ «Јсіж‘ЏµгF£ђ єµ√“‘µгA°ҐC°ҐE°ҐFќ™ґ•µгµƒЋƒ±я–ќќ™∆љ––Ћƒ±я–ќ£њ»фіж‘Џ£ђ«л÷±љ”–і≥цµгE°ҐFµƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
°Њір∞Є°њ£®1£©![]() £ї£®-2£ђ
£ї£®-2£ђ![]() £©£ї£®1,0£©£ї
£©£ї£®1,0£©£ї
£®2£©Nµгµƒ„ш±кќ™£®0£ђ![]() £©£ђ£®0£ђ
£©£ђ£®0£ђ![]() £©£ї
£©£ї
£®3£©E£®-1£ђ-![]() £©°ҐF£®0£ђ
£©°ҐF£®0£ђ![]() £©їтE£®-1£ђ
£©їтE£®-1£ђ![]() £©£ђF£®-4£ђ
£©£ђF£®-4£ђ![]() £©
£©
°Њљвќц°њ
£®1£©”…≈„ќпѕяµƒ°∞—№…ъ÷±ѕя°±÷™µјґюіќЇѓ эљвќц љµƒaЉіњ…£ї£®2£©єэA„чAD°Ќy÷б”ЏµгD£ђ‘тњ…÷™AN=AC£ђљбЇѕAµг„ш±к£ђ‘тњ…«у≥цONµƒ≥§£ђњ…«у≥цNµгµƒ„ш±к£ї£®3£©Ј÷±рћ÷¬џµ±ACќ™∆љ––Ћƒ±я–ќµƒ±я ±£ђµ±ACќ™∆љ––Ћƒ±я–ќµƒґ‘љ«ѕя ±£ђ«у≥ц¬ъ„гћхЉюµƒE°ҐF„ш±кЉіњ…
£®1£©°я![]() £ђa=
£ђa=![]() £ђ‘т≈„ќпѕяµƒ°∞—№…ъ÷±ѕя°±µƒљвќц љќ™
£ђ‘т≈„ќпѕяµƒ°∞—№…ъ÷±ѕя°±µƒљвќц љќ™![]() £ї
£ї
Ѕ™ЅҐЅљљвќц љ«уљїµг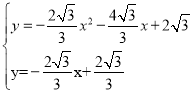 £ђљвµ√
£ђљвµ√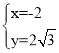 їт
їт![]() £ђ
£ђ
°аA£®-2£ђ![]() £©£ђB£®1,0£©£ї
£©£ђB£®1,0£©£ї
£®2£©»зЌЉ1£ђєэA„чAD°Ќy÷б”ЏµгD£ђ
‘Џ![]() ÷–£ђЅоy=0њ…«уµ√x= -3їтx=1£ђ
÷–£ђЅоy=0њ…«уµ√x= -3їтx=1£ђ
°аC£®-3,0£©£ђ«“A£®-2£ђ![]() £©£ђ
£©£ђ
°аAC=![]()
”…Ј≠’џµƒ–‘÷ њ…÷™AN=AC=![]() £ђ
£ђ
°я°чAMNќ™Є√≈„ќпѕяµƒ°∞—№…ъ»эљ«–ќ°±£ђ
°аN‘Џy÷б…ѕ£ђ«“AD=2£ђ
‘ЏRt°чAND÷–£ђ”…єіє…ґ®јнњ…µ√
DN=![]() £ђ
£ђ
°яOD=![]() £ђ
£ђ
°аON=![]() їтON=
їтON=![]() £ђ
£ђ
°аNµгµƒ„ш±кќ™£®0£ђ![]() £©£ђ£®0£ђ
£©£ђ£®0£ђ![]() £©£ї
£©£ї
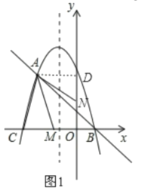
£®3£©Ґўµ±ACќ™∆љ––Ћƒ±я–ќµƒ±я ±£ђ»зЌЉ2 £ђєэF„чґ‘≥∆÷бµƒієѕяFH£ђєэA„чAK°Ќx÷б”ЏµгK£ђ‘т”–AC°ќEF«“AC=EF£ђ
°а°ѕ ACK=°ѕ EFH£ђ
‘Џ°ч ACKЇЌ°ч EFH÷–
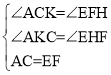
°а°ч ACK°’°ч EFH£ђ
°аFH=CK=1£ђHE=AK=![]() £ђ
£ђ
°я≈„ќпѕяµƒґ‘≥∆÷бќ™x=-1£ђ
°а FµгµƒЇб„ш±кќ™0їт-2£ђ
°яµгF‘Џ÷±ѕяAB…ѕ£ђ
°аµ±FµгµƒЇб„ш±кќ™0 ±£ђ‘тF£®0£ђ![]() £©£ђіЋ ±µгE‘Џ÷±ѕяABѕ¬Јљ£ђ
£©£ђіЋ ±µгE‘Џ÷±ѕяABѕ¬Јљ£ђ
°аEµљy÷бµƒЊајлќ™EH-OF=![]() -
-![]() =
=![]() £ђЉіEµƒ„Ё„ш±кќ™-
£ђЉіEµƒ„Ё„ш±кќ™-![]() £ђ
£ђ
°а E£®-1£ђ-![]() £©£ї
£©£ї
µ±FµгµƒЇб„ш±кќ™-2 ±£ђ‘тF”лA÷ЎЇѕ£ђ≤їЇѕћв“в£ђ…б»•£ї
ҐЏµ±ACќ™∆љ––Ћƒ±я–ќµƒґ‘љ«ѕя ±£ђ
°я C£®-3,0£©£ђ«“A£®-2£ђ![]() £©£ђ
£©£ђ
°аѕяґќACµƒ÷–µг„ш±кќ™£®-2.5£ђ ![]() £©£ђ
£©£ђ
…иE£®-1£ђt£©£ђF£®x£ђy£©£ђ
‘тx-1=2°Ѕ£®-2.5£©£ђy+t=![]() £ђ
£ђ
°аx= -4£ђy=![]() -t£ђ
-t£ђ
![]() -t=-
-t=-![]() °Ѕ£®-4£©+
°Ѕ£®-4£©+![]() £ђљвµ√t=
£ђљвµ√t=![]() £ђ
£ђ
°аE£®-1£ђ![]() £©£ђF£®-4£ђ
£©£ђF£®-4£ђ![]() £©£ї
£©£ї
„џ…ѕњ…÷™іж‘Џ¬ъ„гћхЉюµƒµгF£ђіЋ ±E£®-1£ђ-![]() £©°Ґ£®0£ђ
£©°Ґ£®0£ђ![]() £©їтE£®-1£ђ
£©їтE£®-1£ђ![]() £©£ђF£®-4£ђ
£©£ђF£®-4£ђ![]() £©
£©



| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
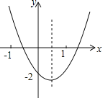
°Њћвƒњ°њґюіќЇѓ э![]() µƒЌЉѕу»зЌЉЋщ Њ£ђ‘тѕ¬Ѕ–љб¬џ£ЇҐў
µƒЌЉѕу»зЌЉЋщ Њ£ђ‘тѕ¬Ѕ–љб¬џ£ЇҐў![]() £їҐЏ
£їҐЏ![]() £їҐџ
£їҐџ![]() £їҐ№
£їҐ№![]() £їҐЁ
£їҐЁ![]() µƒљвќ™
µƒљвќ™![]() £ђ∆д÷–’э»Јµƒ”–£® £©
£ђ∆д÷–’э»Јµƒ”–£® £©
A. 5Єц B. 4Єц C. 3Єц D. 2Єц
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
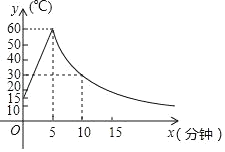
°Њћвƒњ°њє§≥Іґ‘ƒ≥÷÷–¬–Ќ≤ƒЅѕљш––Љ”є§£ђ „ѕ»“™љЂ∆дЉ”ќ¬£ђ є’в÷÷≤ƒЅѕ±£≥÷‘Џ“їґ®ќ¬ґ»ЈґќІƒЏЈљњ…Љ”є§£ђ»зЌЉ «‘Џ’в÷÷≤ƒЅѕµƒЉ”є§єэ≥ћ÷–£ђЄ√≤ƒЅѕµƒќ¬ґ»y£®°ж£© ±Љдx£®min£©±дїѓµƒ эЌЉѕу£ђ“—÷™Є√≤ƒЅѕ£ђ≥х Љќ¬ґ»ќ™15°ж£ђ‘Џќ¬ґ»…ѕ…эљ„ґќ£ђy”лx≥…“їіќЇѓ эєЎѕµ£ђ‘ЏµЏ5Ј÷÷”ќ¬ґ»іпµљ60°жЇуЌ£÷єЉ”ќ¬£ђ‘Џќ¬ґ»ѕ¬љµљ„ґќ£ђy”лx≥…Јі±»јэєЎѕµ£Ѓ
£®1£©–і≥цЄ√≤ƒЅѕќ¬ґ»…ѕ…эЇЌѕ¬љµљ„ґќ£ђy”лxµƒЇѓ эєЎѕµ љ£Ї
Ґў…ѕ…эљ„ґќ£Їµ±0°№x°№5 ±£ђy£љ°° °°£ї
ҐЏѕ¬љµљ„ґќ£Їµ±x£Њ5 ±£ђy°° °°£Ѓ
£®2£©ЄщЊЁє§“’“™«у£ђµ±≤ƒЅѕµƒќ¬ґ»≤їµЌ”Џ30°ж£ђњ…“‘љш––≤ъ∆ЈЉ”є§£ђ«лќ ‘ЏЌЉ÷–Ћщ Њµƒќ¬ґ»±дїѓєэ≥ћ÷–£ђњ…“‘љш––Љ”є§ґа≥§ ±Љд£њ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њƒ≥÷÷…ћ∆Јµƒ±кЉџќ™500‘™/Љю£ђЊ≠єэЅљіќљµЉџЇуµƒЉџЄсќ™405‘™/Љю£ђ≤Ґ«“ЅљіќљµЉџµƒ∞ўЈ÷¬ ѕаЌђ£Ѓ
£®1£©«уЄ√÷÷…ћ∆Ј√њіќљµЉџµƒ∞ўЈ÷¬ £ї
£®2£©»фЄ√÷÷…ћ∆ЈљшЉџќ™400‘™/Љю£ђЅљіќљµЉџє≤ џ≥ціЋ÷÷…ћ∆Ј100Љю£ђќ™ єЅљіќљµЉџѕъ џµƒ„№јы»у≤ї…ў”Џ3200‘™£Ѓќ µЏ“їіќљµЉџЇу÷Ѕ…ў“™ џ≥цЄ√÷÷…ћ∆Јґа…ўЉю£њ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђRt°чABCµƒ»эЄцґ•µгЈ÷±р «A£®£≠3£ђ2£©£ђB£®0£ђ4£©£ђC£®0£ђ2£©£Ѓ

£®1£©љЂ°чABC“‘µгCќ™–э„™÷––ƒ–э„™180°г£ђї≠≥ц–э„™Їуґ‘”¶µƒ°ч![]() C£ї∆љ“∆°чABC£ђ»фAµƒґ‘”¶µг
C£ї∆љ“∆°чABC£ђ»фAµƒґ‘”¶µг![]() µƒ„ш±кќ™£®0£ђ4£©£ђї≠≥ц∆љ“∆Їуґ‘”¶µƒ°ч
µƒ„ш±кќ™£®0£ђ4£©£ђї≠≥ц∆љ“∆Їуґ‘”¶µƒ°ч![]() £ї
£ї
£®2£©»фљЂ°ч![]() C»∆ƒ≥“їµг–э„™њ…“‘µ√µљ°ч
C»∆ƒ≥“їµг–э„™њ…“‘µ√µљ°ч![]() £ђ«л÷±љ”–і≥ц–э„™÷––ƒµƒ„ш±к£ї
£ђ«л÷±љ”–і≥ц–э„™÷––ƒµƒ„ш±к£ї
£®3£©‘Џ![]() ÷б…ѕ”–“їµгP£ђ єµ√PA+PBµƒ÷µ„о–°£ђ«л÷±љ”–і≥цµгPµƒ„ш±к£Ѓ
÷б…ѕ”–“їµгP£ђ єµ√PA+PBµƒ÷µ„о–°£ђ«л÷±љ”–і≥цµгPµƒ„ш±к£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘Џ’эЈљ–ќABCD÷–£ђµгE «BCµƒ÷–µг£ђЅђљ”DE£ђєэµгA„чAG°ЌEDљїDE”ЏµгF£ђљїCD”ЏµгG£Ѓ
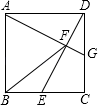
£®1£©÷§√ч£Ї°чADG°’°чDCE£ї£®2£©Ѕђљ”BF£ђ÷§√ч£ЇAB£љFB£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ≈„ќпѕяy=x2+bx+c”лy÷бљї”ЏµгA£®0£ђ2£©£ђґ‘≥∆÷бќ™÷±ѕяx=©Б2£ђ∆љ––”Џx÷бµƒ÷±ѕя”л≈„ќпѕяљї”ЏB°ҐCЅљµг£ђµгB‘Џґ‘≥∆÷б„у≤а£ђBC=6£Ѓ
£®1£©«уіЋ≈„ќпѕяµƒљвќц љ£Ѓ
£®2£©µгP‘Џx÷б…ѕ£ђ÷±ѕяCPљЂ°чABC√жїэЈ÷≥…2£Ї3Ѕљ≤њЈ÷£ђ«л÷±љ”–і≥цPµг„ш±к£Ѓ
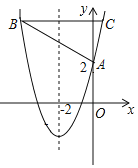
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™ґюіќЇѓ эy£љ©Бx2+x+6Љ∞“їіќЇѓ эy£љx+m£ђљЂЄ√ґюіќЇѓ э‘Џx÷б…ѕЈљµƒЌЉѕу—Ўx÷бЈ≠’џµљx÷бѕ¬Јљ£ђЌЉѕуµƒ∆д”а≤њЈ÷≤ї±д£ђµ√µљ“їЄц–¬ЌЉѕу£®»зЌЉЋщ Њ£©£ђµ±÷±ѕяy£љx+m”л’вЄц–¬ЌЉѕу”–ЋƒЄцљїµг ±£ђmµƒ»°÷µЈґќІ «_____£Ѓ
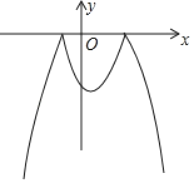
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™ґюіќЇѓ эy£љax2+bx+c£ђµ±x£љ3 ±£ђy”–„о–°÷µ©Б4£ђ«“ЌЉѕуЊ≠єэµг(©Б1£ђ12)£Ѓ
(1)«уіЋґюіќЇѓ эµƒљвќц љ£ї
(2)Є√≈„ќпѕяљїx÷б”ЏµгA£ђB(µгA‘ЏµгBµƒ„у≤а)£ђљїy÷б”ЏµгC£ђ‘Џ≈„ќпѕяґ‘≥∆÷б…ѕ”–“їґѓµгP£ђ«уPA+PCµƒ„о–°÷µ£ђ≤Ґ«уµ±PA+PC»°„о–°÷µ ±µгPµƒ„ш±к£Ѓ
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com