
����Ŀ��С��Ͷ������һ�ֽ���Ϊÿ��20Ԫ�Ļ���̨�ƣ������г����з��֣�ÿ�����۵�����y���������ۼ�x��Ԫ/������һ�κ��������Ӧ��ϵ�����
x/��Ԫ/���� | 22 | 25 | 30 | 35 | �� |
y/�� | 280 | 250 | 200 | 150 | �� |
�����۹��������۵��۲����ڳɱ��ۣ���۾ֹ涨ÿ����Ʒ�����ø��ڳɱ��۵�60%��
��1�������y����x�ĺ�����ϵʽ��
��2����С��ÿ�»������Ϊw��Ԫ������ÿ�»������w��Ԫ�����ۼ�x��Ԫ/����֮��ĺ�����ϵʽ����ȷ���Ա���x��ȡֵ��Χ��
��3�����ۼ۶�Ϊ����Ԫ/��ʱ��ÿ�¿ɻ�����������������Ƕ��٣�
���𰸡���1��y����10x+500����2��w����10x2+700x��10000��20��x��32������3�����ۼ۶�Ϊ32Ԫ/��ʱ��ÿ�¿ɻ������������������2160Ԫ��
��������
��1��ֱ�����ô���ϵ����������⣻
��2������ÿ�»������=ÿ����Ʒ������![]() ÿ�����۵�����������⣻
ÿ�����۵�����������⣻
��3�����ݶ��κ����������Լ�����⣮
�⣺��1����y��x�ĺ�����ϵʽΪy��kx+b��
![]() ����
����![]() ��
��
��y��x�ĺ�����ϵʽΪy����10x+500��
��2��������ɵã�
w����x��20��y����x��20������10x+500������10x2+700x��10000��
�������۹��������۵��۲����ڳɱ��ۣ���۾ֹ涨ÿ����Ʒ�����ø��ڳɱ��۵�60%��
��x��20��x��20��20��60%��
��20��x��32��
��ÿ�»������w��Ԫ�����ۼ�x��Ԫ/����֮��ĺ�����ϵʽ��w����10x2+700x��10000��20��x��32����
��3����w����10x2+700x��10000����10��x��35��2+2250��20��x��32��
�൱x��32ʱ��wȡ�����ֵ����ʱw��2160��
�𣺵��ۼ۶�Ϊ32Ԫ/��ʱ��ÿ�¿ɻ������������������2160Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ����������
����������![]() ��
��![]() ��
��![]() �ֱ�Ϊ��
�ֱ�Ϊ��![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
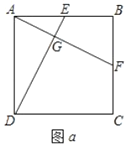
��1����֤��![]() ��
��
��2����ͼ![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
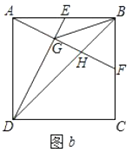
����֤��![]() ��
��
����![]() ����������
����������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ��![]() ���������н��ۣ�
���������н��ۣ�
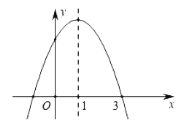
��![]() �� ��
�� ��![]() �� ��
�� ��![]() �� ��
�� ��![]() ��
��
���У���ȷ�Ľ����У� ��
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ѧ�����ۺ�������ijУ�����������ֹ���Σ���������Ϊ��![]() ����ֽ����
����ֽ����![]() ��ɳ������
��ɳ������![]() ����«��̡���
����«��̡���![]() �����ܡ���
�����ܡ���![]() ���廨����Ϊ���˽�ѧ����ÿ�ֻ�ε�ϲ������������ȡ�˲���ͬѧ���е��飬�����������Ƴ�����������������ͳ��ͼ��
���廨����Ϊ���˽�ѧ����ÿ�ֻ�ε�ϲ������������ȡ�˲���ͬѧ���е��飬�����������Ƴ�����������������ͳ��ͼ��
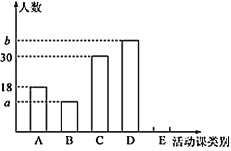

����������Ϣ���ش��������⣺
��1�����ε������������Ϊ________��ͳ��ͼ�е�![]() ________��
________��![]() ________��
________��
��2��ͨ�����㲹ȫ����ͳ��ͼ��
��3����У����2500��ѧ�����������ȫУϲ������«��̡���ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��Ե�A��0��2��ΪԲ�ģ�2Ϊ�뾶��Բ��y���ڵ�B����֪��C��2��0������DΪ��A�ϵ�һ���㣬��CDΪб�ߣ���CD���������ֱ��������CDE������BC������BCE�������СֵΪ_____��
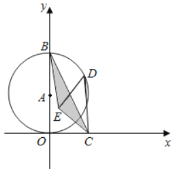
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��-3,0������B��0��![]() ����ֱ��
����ֱ��![]() ��x�ᡢy��ֱ��ڵ�D��C��M��ƽ����һ���㣬�ҡ�AMB=60�㣬��MCD�������Сֵ�� ________��
��x�ᡢy��ֱ��ڵ�D��C��M��ƽ����һ���㣬�ҡ�AMB=60�㣬��MCD�������Сֵ�� ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB��AC��2![]() ��BC��8�������в�����ͼ��
��BC��8�������в�����ͼ��
���Ե�AΪԲ�ģ��ʵ��ij���Ϊ�뾶�������ֱ�AB��AC�ڵ�E��F���ٷֱ��Ե�E��FΪԲ�ģ�����![]() EF�ij�Ϊ�뾶�����ཻ�ڵ�H��������AH��
EF�ij�Ϊ�뾶�����ཻ�ڵ�H��������AH��
�ڷֱ��Ե�A��BΪԲ�ģ�����![]() AB�ij�Ϊ�뾶�����ཻ�ڵ�M��N����ֱ��MN��������AH�ڵ�O��
AB�ij�Ϊ�뾶�����ཻ�ڵ�M��N����ֱ��MN��������AH�ڵ�O��
���Ե�OΪԲ�ģ��߶�OA��Ϊ�뾶��Բ��
���O�İ뾶Ϊ��������
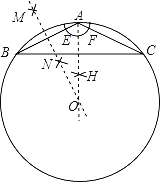
A.2![]() B.10C.4D.5
B.10C.4D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿ�����ˮ��ʶ����������ˮ��˾�����Ի�Ϊ��λ�ֶμƷѰ취�շѣ���ÿ����ˮ������10�֣�ÿ���շ�![]() Ԫ��������10�֣���10��ˮ��ÿ��
Ԫ��������10�֣���10��ˮ��ÿ��![]() Ԫ�շѣ�����10�ֵIJ��ְ�ÿ��
Ԫ�շѣ�����10�ֵIJ��ְ�ÿ��![]() Ԫ�շѣ���˾Ϊ������Ƶ�ˮ��
Ԫ�շѣ���˾Ϊ������Ƶ�ˮ��![]() ��Ԫ���뵱����ˮ��
��Ԫ���뵱����ˮ��![]() ���֣�֮��ĺ���ͼ�����£������н��۴�����ǣ� ��
���֣�֮��ĺ���ͼ�����£������н��۴�����ǣ� ��
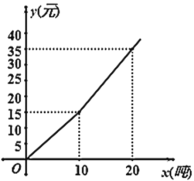
A.![]()
B.![]()
C.��С����3�·���ˮ14�֣���Ӧ��ˮ��23Ԫ
D.��С����7�·ݽ�ˮ��30Ԫ������û�������ˮ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ������
��ֱ������![]() ��
��![]() ��һ�㣬
��һ�㣬![]() ����
����![]() �������ഹֱ������Ϊ��
�������ഹֱ������Ϊ��![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ӳ����ཻ�ڵ�
���ӳ����ཻ�ڵ�![]() ����
����![]() ƽ��
ƽ��![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
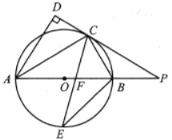
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2��̽���߶�![]() ��
��![]() ֮��Ĵ�С��ϵ��������֤����
֮��Ĵ�С��ϵ��������֤����
��3����![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com