
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,
上一点,![]() 和过点
和过点![]() 的切线互相垂直,垂足为点
的切线互相垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .弦
.弦![]() 平分
平分![]() ,交直径
,交直径![]() 于点
于点![]() ,连接
,连接![]() .
.
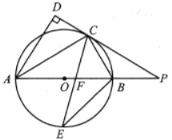
(1)求证:![]() 平分
平分![]() ;
;
(2)探究线段![]() ,
,![]() 之间的大小关系,并加以证明;
之间的大小关系,并加以证明;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]()
【解析】
(1)连接OC,根据切线的性质可得OC⊥CD,则AD∥OC,根据等边对等角,以及平行线的性质即可证得;
(2)根据圆周角定理以及三角形的外角的性质定理证明∠PFC=∠PCF,根据等角对等边即可证得;
(3)证明△PCB∽△PAC,根据相似三角形的性质求得PB与PC的比值,在直角△POC中利用勾股定理即可列方程求解.
解:(1)连接OC.
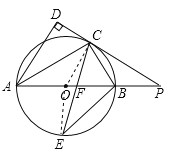
∵OA=OC,
∴∠OAC=∠OCA.
∵PC是⊙O的切线,AD⊥CD,
∴∠OCP=∠D=90°,
∴OC∥AD.
∴∠CAD=∠OCA=∠OAC.即AC平分∠DAB.
(2)PC=PF.
证明:∵AB是直径,
∴∠ACB=90°,
∴∠PCB+∠ACD=90°
又∵∠CAD+∠ACD=90°,
∴∠CAB=∠CAD=∠PCB.
又∵∠ACE=∠BCE,∠PFC=∠CAB+∠ACE,∠PCF=∠PCB+∠BCE.
∴∠PFC=∠PCF.
∴PC=PF.
(3)连接AE.
∵∠ACE=∠BCE,
∴![]() ,
,
∴AE=BE.
又∵AB是直径,
∴∠AEB=90°.
AB= ![]() BE=10,
BE=10,
∴OB=OC=5.
∵∠PCB=∠PAC,∠P=∠P,
∴△PCB∽△PAC.
∴![]() .
.
∵tan∠PCB=tan∠CAB=![]() .
.
∴![]() .
.
设PB=3x,则PC=4x,在Rt△POC中,(3x+5)2=(4x)2+52,
解得x1=0,x2=![]() .
.
∵x>0,∴x=![]() ,
,
∴PF=PC=![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.经过市场调研发现,每月销售的数量y(件)是售价x(元/件)的一次函数,其对应关系如表:
x/(元/件) | 22 | 25 | 30 | 35 | … |
y/件 | 280 | 250 | 200 | 150 | … |
在销售过程中销售单价不低于成本价,物价局规定每件商品的利润不得高于成本价的60%,
(1)请求出y关于x的函数关系式.
(2)设小明每月获得利润为w(元),求每月获得利润w(元)与售价x(元/件)之间的函数关系式,并确定自变量x的取值范围.
(3)当售价定为多少元/件时,每月可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的高速发展,人们的支付方式发生了巨大改变,某学习小组抽样调查了春节期间某商场顾客的支付方式,主要有现金支付、银联卡支付和手机支付,调查得知使用这三种支付的人数比为![]() ,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:
,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:![]() ~支付宝,
~支付宝,![]() ~微信,
~微信,![]() ~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.
~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.

(1)扇形统计图中,![]() ________;请补全条形统计图;
________;请补全条形统计图;
(2)若该商场春节期间共20000人购物,请估计用支付宝进行支付的人数.
(3)经调查某天顾客现金支付、银联卡支付、手机支付每笔交易发生的平均金额分别为120元、260元、80元,求这天顾客每笔交易的平均金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
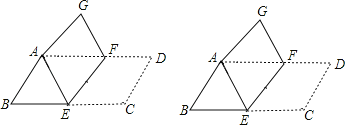
【题目】如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.
(1)连接CF,求证:四边形AECF是菱形;
(2)若E为BC中点,BC=26,tan∠B=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
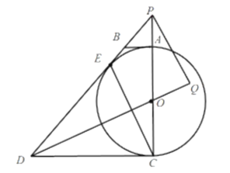
【题目】如图,在![]() 中,
中,![]() 是直径,
是直径,![]() 是切线,点
是切线,点![]() 为切点.
为切点.
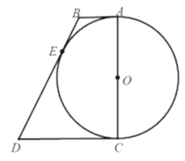
(1)求证:![]() ;
;
(2)如图,连接![]() 交于点
交于点![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;

(3)如图,延长![]() 交于点
交于点![]() 连接
连接![]() 过点
过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .若
.若![]()
![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分):
项目人员 | 阅读能力 | 思维能力 | 表达能力 |
甲 | 93 | 86 | 73 |
乙 | 95 | 81 | 79 |
(1)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
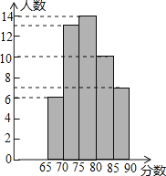
(2)公司按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com